Основы цифровой техники. Основные законы алгебры логики

Цифровыми называются устройства обработки информации, в которых информация представлена в цифровой форме, т.е. в виде цифрового кода (электрических сигналов с ограниченным множеством дискретных значений амплитуды в дискретном пространстве времени).

Чаще всего используется двоичное (бинарное) кодирование, когда электрический сигнал принимает два значения: низкий (минимально возможный уровень) и высокий (максимально возможный уровень), т.е. двоичная система счисления и связанный с ней математический аппарат, так называемая алгебра логики или булева алгебра (по имени ее основоположника Д. Буля). Такие сигналы имеют максимальное возможное кодовое расстояние, следовательно, система обработки информации будет иметь высокую помехоустойчивость.

В алгебре логики рассматривают переменные и функции от них, которые принимают только два значения: ложь (False) или истина (True). Их принято называть логическими переменными и логическими функциями. В двоичной позиционной системе счисления любое число также записывается с помощью двух символов (цифр) 0 и 1.

Это обстоятельство позволяет, используя только два символа 0 и 1, записывать и выполнять логические и арифметические операции, т.е. выполнять цифровую обработку электрических сигналов, имеющих по амплитуде два уровня. Если высокий уровень электрического сигнала принимается за 1 (истина), а низкий уровень за 0 (ложь), то считается, что это положительная логика, если же низкий соответствует 1, а высокий - 0, то логика считается отрицательной.

Арифметические операции в двоичной арифметике аналогичны всем известным операциям с десятичными числами. В табл. 5.1 отражено соответствие четырехразрядных двоичных (В), одноразрядных шестнадцатеричных (Н) и двухразрядных десятичных чисел. Например, двоичное число (двоичный код числа) 1111 1111 1100 0101В в шестнадцатеричной форме записывается как FFC5H и соответствует десятичному числу (десятичному коду) 15*16³ +15*16² +12*16¹ +5*16⁰ = 65477, где 16 - основание шестнадцатеричной позиционной системы счисления, а показатель его степени - номер позиции.

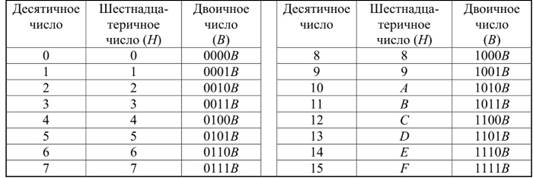
Таб. 5.1. Соответствие десятичных, шестнадцатеричных и двоичных чисел

В алгебре логики определены:
- отношение эквивалентности (тождественность), обозначаемое знаком "=" (равно), например: F(x) = x₁ y и четыре основные логические операции:

- отрицание (иначе - инверсия, операция НЕ), обозначаемая чертой над переменной и читаемое как "НЕ х", например: F(x) = x
- дизъюнкция (логическое сложение, операция ИЛИ), обозначаемая знаками "\/", или "+", или "|", например: F(x₁, x₂) = x₁ \/ x₂ = x₁ + x₂ = x₁ l x₂;

- конъюнкция (логическое умножение, операция И), обозначаемая знаками "/\" или "^." или "&", например: F(x₁, x₂) = x₁ /\ x₂ = x₁ ^. x₂ = x₁ & x₂.
- исключающее ИЛИ (сумма по модулю два, неравнозначность), обозначаемое знаком " 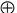", например: F(x₁, x₂) = х₁ 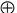х₂

Логические функции могут быть представлены словесно, таблично, алгебраически или графически. Таблично логические функции представляются в виде таблиц истинности, которые содержат все возможные наборы значений логических переменных и значения функций, соответствующих каждому из этих наборов. Поскольку и функции, и их аргументы (переменные) могут принимать только два значения, то, при числе переменных n, может существовать 2^п наборов переменных и 2²ⁿ различных функций. Например, при п = 1 получим четыре логические функции: F₁(x)=0, F₂(x)=1 (тождественность константе), F₃(x)=x₁ (тождественность x₁), F₄(x) =x1 (тождественность НЕ x₁).

Для функций двух переменных x₁ и x₂ возможно существование уже 16 логических функций, приведенных в таблице истинности 5.2 и т.д. Функции F₁(x₁, x₂)=0 и F₂(x₁ x₂)=1 это вырожденные функции, представляющие собой константы, функции F₃(x₁, x₂)= х₁, F₄(x₁ x₂)= x₁, F₅(x_1t x₂) = х₂ и F₆(x₁, x₂)= x₂ зависят от одной переменной, функция F₇(x₁, x₂)= x₁ /\ x₂=x₁+x₂ это дизъюнкция переменных x₁ и x₂, функция F₈(x₁, x₂)= x₁/\x₂=x₁^.x₂=x₁&x₂ это конъюнкция переменных x₁ и x₂, функция F₉(x₁ x₂)= x₁ 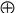х₂ - сумма по модулю два (исключающее ИЛИ, неравнозначность) переменных x₁ и x₂, функция F₁₀(x₁, x₂)= x₁ 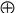х₂ - равнозначность, функция F₁₁(x₁, x₂)= x₁lx₂= x₁ + х₂ носит название операции ИЛИ-НЕ (функции Вебба, стрелки Пирса), функция F₁₂(x₁ x₂)= x₁/x₂= х₁^.х₂ носит название операции И-НЕ (функции Шеффера, штриха Шеффера), функции F₁₃ - F₁₆ названий не имеют.

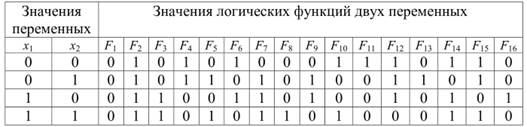
Таб. 5.2. Сводная таблица истинности для логических функций двух переменных

Логические функции преобразуются с целью их упрощения с помощью аксиом и законов алгебры логики, которые доказываются подстановкой возможных значений переменных в таблицы истинности. Основные аксиомы и законы алгебры логики приведены в табл. 5.3.

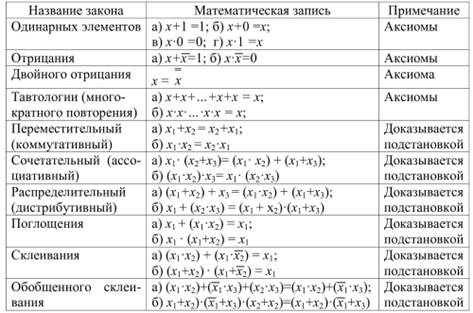
Таб. 5.3. Основные законы алгебры логики

В алгебре логики существуют также несколько теорем, применяемых при преобразовании логических выражений, важнейшие из них - теоремы де Моргана:

1. Инверсия дизъюнкции переменных равна конъюнкции их инверсий: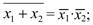
2. Инверсия конъюнкции переменных равна дизъюнкции их инверсий:

Обобщением этих теорем является закон двойственности: Инверсия любой булевой функции равна этой булевой функции с одновременной взаимной заменой каждой переменной на ее инверсию и операций дизъюнкции и конъюнкции.

Используя теоремы де Моргана и закон двойственности любую, сколь угодно сложную, логическую функцию можно представить в совершенно дизъюнктивной нормальной форме (СДНФ), те. записать, используя только операции дизъюнкции, либо в совершенно конъюнктивной нормальной форме (СКНФ), т.е. записать, используя только операции конъюнкции.

Также как и в математике в алгебре логики имеется старшинство операций. Порядок выполнения операций следующий:
1. Действия в скобках;
2. Операции с одним операндом (одноместная операция НЕ);
3. Конъюнкция (операции И);
4. Дизъюнкция - (операции ИЛИ);
5. Сумма по модулю два.

Операции одного ранга выполняются слева направо в порядке написания логического выражения. Более подробно с алгеброй логики можно познакомиться в курсе дискретной математики, но, используя вышеизложенное, уже можно решить простые задачи минимизации логических функций, т.е. нахождения таких их форм, которые эквивалентны исходным, но содержат минимальное число переменных (используя, например, законы склеивания) и минимальное число операций с ними.

Алгебра логики линейна и для неё справедлив принцип суперпозиции. Любую, сколь угодно сложную, логическую функцию можно представить с помощью комбинации нескольких простейших функций. Такой набор простейших логических функций называют функционально полным логическим базисом, или просто базисом. Несложно доказать, что функционально полными будут пять систем таких простейших функций (базисов):

1) Набор из трех функций: НЕ, И, ИЛИ;
2) Набор из двух функций: НЕ, ИЛИ;
3) Набор из двух функций: НЕ, И;
4) Набор из одной функции Вебба: ИЛИ-НЕ;
5) Набор из одной функции Шеффера: И-НЕ

Для реализации цифровых систем любой сложности достаточно иметь набор логических элементов, т.е. электронных схем, реализующих все операции хотя бы одного из этих пяти наборов. В интегральной схемотехнике преимущественное распространение получили логические элементы потенциального типа.

Связь потенциальных логических элементов друг с другом, предыдущими и последующими узлами в цифровой электронной системе осуществляется непосредственно, без применения реактивных компонентов (конденсаторов и трансформаторов), что позволяет выполнить их в интегральном исполнении. В микроэлектронике решающее значение имеет не сложность элементов, а число их типов (чем больше разновидностей, тем дороже изготовление схемы), поэтому наибольшее распространение получили логические элементы ИЛИ-НЕ и И-НЕ, т.е. 4 и 5 базисы, изготавливаемые по различным технологиям на основе биполярных и полевых транзисторных структур.

Такие логические элементы в интегральном исполнении называются базовыми логическими элементами. Используя такие базовые элементы, строят серии логических микросхем с логическими элементами и другими схемами любой степени сложности, в том числе и микропроцессоры.