Поверхности вращения

Поверхности второго порядка.

Содержание лекции: Поверхности в пространстве: конические, цилиндрические, вращения. Поверхности второго порядка: сфера, конус, гиперболоиды, эллипсоид, параболоиды, цилиндрические поверхности. Канонические уравнения поверхностей.

В трехмерном пространстве уравнение вида 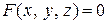определяет некоторую поверхность. Так, мы уже знаем уравнение поверхности первого порядка – плоскости .

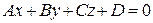Алгебраическое уравнение второго и выше порядков определяет в пространстве поверхности, которые так и называют поверхностями второго и более высоких порядков. Рассмотрим поверхности второго порядка и их простейшие уравнения.

Поверхности вращения

Определение 1

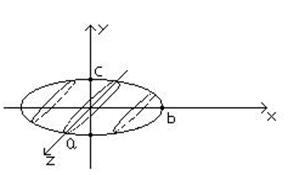
Поверхностью вращения называется поверхность, образованная вращением некоторой пространственной линии L (называемой образующей) вокруг заданной прямой l (называемой осью вращения), лежащей в одной плоскости с L (рисунок 1).

Очевидно, при вращении L каждая точка её описывает окружность.

Простейший случай поверхности вращения, когда кривая L вращается вокруг оси координат.

Поверхности, образованные вращением кривых второго порядка вокруг их осей симметрии, называют поверхностями вращения второго порядка.

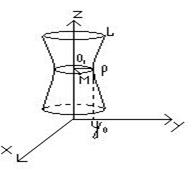Пусть кривая L, лежащая в плоскости уOz, вращается вокруг оси Oz. Уравнения этой кривой можно записать в виде:

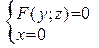
Пусть S - поверхность вращения, M(x, y, z) – произвольная точка этой поверхности. Проведём плоскость a 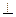Oz, проходящую через точку M. Пусть O₁ точка пересечения плоскости a с Oz, а точка P – с кривой L. Тогда O₁ (0,0,z), а P(0, y₀, z), где y₀- некоторое число.

В сечении поверхности S плоскостью a получается окружность; точки P и M лежат на этой окружности, причём радиус окружности равен |O₁M|=|O₁P|. Имеем |O₁P| = | y₀| (так как LÎyOz), значит, с одной стороны O₁M|= | y₀|. В то же время

|O₁M|= = .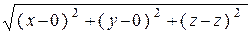

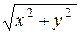Следовательно, |y₀|= 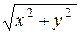, или у₀ = ± 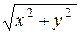. А так как PÎL, то её координаты удовлетворяют уравнениям кривой: 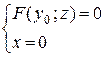, отсюда F(y₀, z)= 0. Представив сюда y₀=± 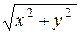, получим

F = (± 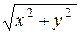; z)=0,

значит координаты произвольной точки M(x, y, z), лежащей на поверхности вращения удовлетворяет уравнению F = (± 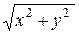; z) = 0, значит, это уравнение есть уравнение поверхности S.

Аналогично можно вывести уравнение поверхности вращения вокруг других осей.

Отсюда мы можем вывести следующее практическое правило:

Чтобы найти уравнение поверхности вращения кривой L вокруг координатной оси, лежащей с L в одной плоскости, нужно в уравнении кривой L переменную, соответствующую оси вращения, оставить без изменения, а вторую переменную заменить на (±) корень квадратный из суммы квадратов остальных переменных.

Например, если L: F (x, y) = 0, LÎxOy и вращается вокруг оси Oy, то уравнение поверхности вращения F = (± 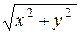; z) = 0. Если эта кривая вращается вокруг оси Ox, то уравнение поверхности запишется в виде F = (x;± 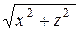) = 0. Если L: F (x, z) = 0 вращается вокруг Oz, то поверхность имеет уравнение F = (± 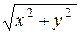; z)=0 и т.д.

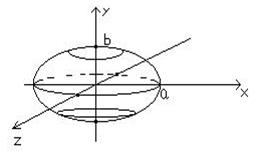
Например, при вращении окружности (у – a)² + z² =1 вокруг оси Оy получится шар, а при вращении вокруг оси OZ – тор (рис.)

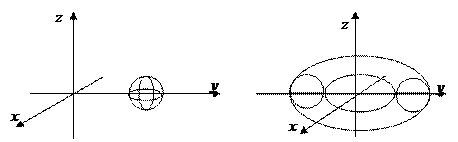Особенности: в сечении поверхности вращения плоскостями, ^ оси вращения, получаются окружности.

Рассмотрим поверхности, которые получаются при вращении кривых второго порядка.

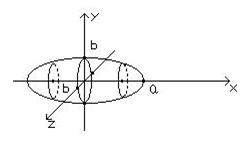1) 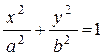- эллипс с полуосями a и b. Если вращать его вокруг оси Oх, то получим поверхность с уравнением

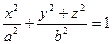, или .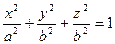

Эта поверхность называется эллипсоидом вращения. Здесь, очевидно, ± a – отрезки, который “отсекает” эллипсоид на оси Oх, ± b- отрезки на осях Oу, Oz, числа a, b , b в этом случае называются полуосями эллипсоида.

Аналогично, вращая эллипс 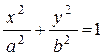вокруг Oy, получим поверхность 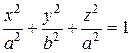- та же структура уравнения, значит, это также эллипсоид вращения с полуосями a и b. Отличительная особенность уравнения эллипсоида вращения: сумма, 3 квадрата, две полуоси одинаковые. По этим признакам можно узнать тип поверхности.

Например: 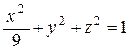– эллипсоид вращения: эллипс 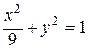вращается вокруг оси OX.

Если деформировать эллипсоид 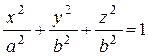вдоль оси Oz (сжать или растянуть), то уравнение приобретает вид

,

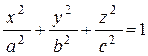этот эллипсоид называется трехосным эллипсоидом, a, b, c- полуоси эллипсоида.

2) Рассмотрим гиперболу 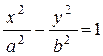. Если вращать её вокруг оси Oy, то получим поверхность с уравнением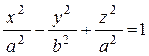

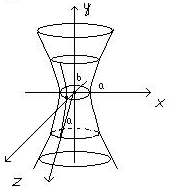Поверхность такого вида называется однополостным гиперболоидом вращения, a, b, a- полуоси гиперболоида. Если деформировать поверхность вдоль оси z; получим поверхность

,

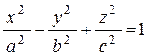которая называется просто однополостным гиперболоидом.

Отличительные особенности: 3 квадрата, один минус остальные плюсы, справа 1.

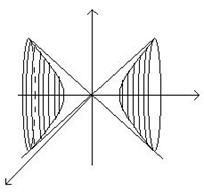
Если гиперболу 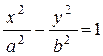вращать вокруг оси Ox, получим поверхность с уравнением ,

у

х

Эта поверхность называется двуполостным гиперболоидом вращения. Если деформировать его, получим просто двуполостный гиперболоид

.,

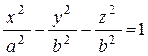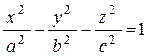Отличительные особенности: 3 квадрата, 2 минуса, справа 1.

3) Рассмотрим параболу 2pz = у² и будем вращать её вокруг оси Oz, получим поверхность с уравнением x² + y² = 2pz, или 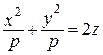– параболоид вращения.

Если теперь деформировать эту поверхность вдоль оси Оу, получим поверхность с уравнением 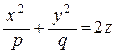, p, q >0, которая называется эллиптическим параболоидом