Цилиндрические поверхности.
Пусть L - некоторая линия в пространстве, а l – прямая, не лежащая с L в одной плоскости.
Определение 8.2.
Цилиндрической поверхностью называется множество точек пространства, являющееся объединением всех прямых, параллельных заданной прямой l и проходящих через точки кривой L. Линия L называется направляющей, а прямые, параллельные прямой l- образующими цилиндра.
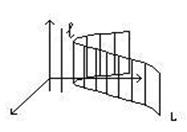
 Рассмотрим цилиндрические поверхности с образующими, параллельными осям координат, а направляющими, лежащими в координатных плоскостях.
Рассмотрим цилиндрические поверхности с образующими, параллельными осям координат, а направляющими, лежащими в координатных плоскостях.
Пусть L: 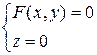 - кривая в пространстве (очевидно, она лежит в плоскости xOy), а l = Oz.
- кривая в пространстве (очевидно, она лежит в плоскости xOy), а l = Oz.
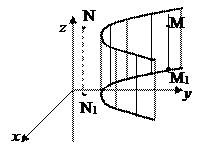
Рассмотрим цилиндрическую поверхность. Пусть M(x, y, z) – произвольная точка этой поверхности. Тогда проекция M1 (x, y, 0) этой точки на плоскость xOy лежит на направляющей L. Значит, её координаты x и y удовлетворяют уравнению L:
F (x, y) = 0.
Наоборот, если точка N(x1, y1, z1) не принадлежит цилиндрической поверхности, то F (x1, y1) ¹ 0 (N  ÏL), то есть уравнению F (x, y) = 0, удовлетворяют координаты точек цилиндрической поверхности и только они, следовательно, F (x, y) = 0 есть уравнение цилиндрической поверхности с направляющей
ÏL), то есть уравнению F (x, y) = 0, удовлетворяют координаты точек цилиндрической поверхности и только они, следовательно, F (x, y) = 0 есть уравнение цилиндрической поверхности с направляющей 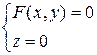 и образующей, параллельной Oz.
и образующей, параллельной Oz.
Аналогично можно показать, что уравнение F(x,z)=0 определяет цилиндрическую поверхность с образующей, параллельной Oy и направляющей 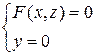
Уравнение F (y,z)=0 определяет цилиндрическую поверхность с направляющей 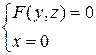 и образующей, параллельной оси Ox.
и образующей, параллельной оси Ox.
Цилиндрическая поверхность, у которой направляющая есть кривая 2-го порядка, называется цилиндрической поверхностью 2-го порядка.
 Например, поверхность
Например, поверхность 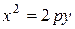 (или
(или 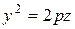 ) называется параболическим цилиндром.
) называется параболическим цилиндром.
 Поверхность с уравнением
Поверхность с уравнением 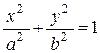 или
или 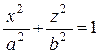 - эллиптический цилиндр:
- эллиптический цилиндр:

 Уравнения
Уравнения 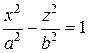 и
и 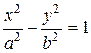 определяют гиперболический цилиндр:
определяют гиперболический цилиндр:
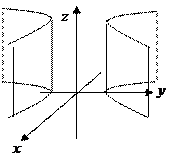 |
Дата добавления: 2022-02-05; просмотров: 338;











