Конические поверхности.
Пусть L - некоторая кривая и точка AÏL и не лежит с L в одной плоскости. Рассмотрим множество точек лежащих на прямых AM, где M – произвольная точка кривой L, это множество точек называется конусом с вершиной в точке A и направляющей L.
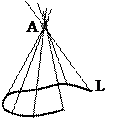 Определение 3.
Определение 3.
Поверхность, образованная прямыми линиями, проходящими через заданную точку А и точки кривой L, называется конической поверхностью или конусом.Точка А называется вершиной конуса, кривая L – направляющей, прямые АМ, где МÎL, называются образующими конуса.
 Если направляющая конуса есть кривая второго порядка, не лежащая в одной плоскости с вершиной, то конус называется конусом второго порядка.
Если направляющая конуса есть кривая второго порядка, не лежащая в одной плоскости с вершиной, то конус называется конусом второго порядка.
Например, если направляющей конуса является эллипс 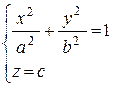 , а вершина – начало координат, то уравнение конуса имеет вид
, а вершина – начало координат, то уравнение конуса имеет вид 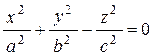 , это конус 2-го порядка.
, это конус 2-го порядка.
Поверхности второго порядка.
Определение 4.
Поверхностью второго порядка называется поверхность, которая в декартовой системе координат описывается уравнением второго порядка
Ах2 + Ву2 + Сz2 + Dxy + Exz + Fyz + Mx +Ny + Hz +P = 0, (1)
где хотя бы одно из чисел А, В, С, D, E, F не равно нулю.
Рассмотренные выше поверхности:
конус 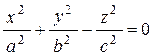 , эллипсоид
, эллипсоид 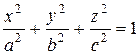 , однополостный гиперболоид
, однополостный гиперболоид 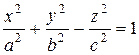 , двуполостный гиперболоид
, двуполостный гиперболоид 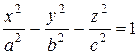 , эллиптический параболоид
, эллиптический параболоид 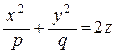 , цилиндры:
, цилиндры: 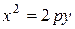 ,
, 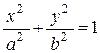 ,
, 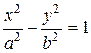 – являются поверхностями второго порядка. Записанные уравнения этих поверхностей называются каноническими уравнениями.
– являются поверхностями второго порядка. Записанные уравнения этих поверхностей называются каноническими уравнениями.
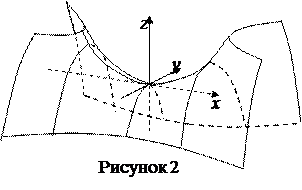 Доказано, что кроме перечисленных, к поверхностям второго порядка относится поверхность с уравнением
Доказано, что кроме перечисленных, к поверхностям второго порядка относится поверхность с уравнением 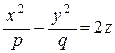 , p, q > 0, она называется гиперболическим параболоидом (рисунок 2).
, p, q > 0, она называется гиперболическим параболоидом (рисунок 2).
Других поверхностей второго порядка, кроме случая вырождения (плоскости, пары плоскостей, прямой, точки, пустого множества), не существует. Причем канонические уравнения этих поверхностей получаются в том случае, когда система координат выбрана так, что оси координат являются осями симметрии поверхности. В общем случае поверхности второго порядка описываются уравнением вида (1), которое называется общим уравнением поверхности второго порядка.
Чтобы определить, какую поверхность описывает общее уравнение (1), нужно либо преобразовать его к каноническому виду (с помощью преобразования системы координат), либо использовать метод сечений.
Суть этого метода заключается в том, что рассматривают сечения поверхности 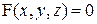 координатными плоскостями и плоскостями, параллельными им. Форма, размеры и взаимное расположение полученных сечений позволяют выяснить форму самой поверхности.
координатными плоскостями и плоскостями, параллельными им. Форма, размеры и взаимное расположение полученных сечений позволяют выяснить форму самой поверхности.
Все перечисленные выше поверхности второго порядка и их канонические уравнения приведены в таблице:
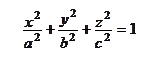  
|
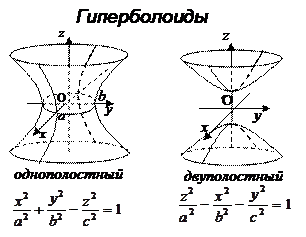
|
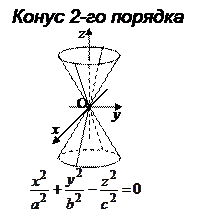
| 
|
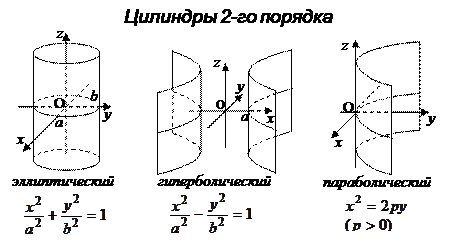
|
Дата добавления: 2022-02-05; просмотров: 280;











