Математическое введение в цифровую технику.
1-1. Системы счисления, используемые в цифровой технике.
Для изображения чисел используются определенные приемы и правила, называемые системами счисления. Все известные системы счисления делятся на две группы: позиционные системы счисления и непозиционные системы счисления.
В непозиционной системе счисления значение символа (цифры, буквы, знака или иероглифа) постоянно и не зависит от позиции этого символа в изображаемом числе. В позиционных системах наоборот, значение символа зависит от позиции этого символа в изображаемом числе. Непозиционные системы, как более простые, появились исторически гораздо более раньше позиционных систем. Ими пользовались древние славяне, китайцы и другие народы. До наших дней дошла одна из разновидностей непозиционных систем - римская система счисления. В ней используются так называемые римские цифры: I- 1, V- 5, X- 10, L- 50, C- 100, D- 500, M- 1000. Значение числа вычисляется суммированием всех чисел с учетом правила, что если цифра меньшего веса стоит слева от следующей за ней цифрой большего веса, то она имеет знак минус, а если справа - то знак плюс. Например, число MCCXXXIV определяется следующим образом:
1000 + 100 + 100 + 10 + 10 + 10 - 1 + 5 = 1234
Непозиционные системы счисления обладают двумя существенными недостатками. Во-первых, при увеличении диапазона представляемых чисел увеличивается число различных символов в изображаемых числах. Во-вторых, очень сложны правила выполнения даже самых простых арифметических действий.
Позиционные системы счисления обладают тем чрезвычайно важным свойством, что все числа, и малые, и большие, могут быть записаны с помощью конечного набора различных символов. Кроме того, правила действия с числами могут быть резюмированы в виде таблиц сложения и умножения. Изобретение позиционных систем счисления имело неоценимые последствия для дальнейшего развития человеческой цивилизации. Впервые такие системы счисления стали использовать древние шумерийцы и индусы.
В позиционных системах счисления любое число X изображается в виде полинома
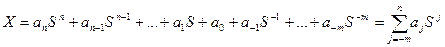 . (1.1)
. (1.1)
B этом выражении aj называются разрядными коэффициентами, S - основанием системы счисления, а Sj – весовыми коэффициентами. Значение любого разрядного коэффициента в изображаемом числе может лежать в диапазоне от 0 до S-1. В настоящее время во всех странах мира используется десятичная система счисления, представляющая собой позиционную систему счисления с основанием S=10. Разрядные коэффициенты при изображении чисел в десятичной системе счисления могут принимать значения в диапазоне от 0 до 9. Для краткости вместо записи числа в виде полинома записывают только последовательность разрядных коэффициентов этого полинома. Когда мы пишем десятичное число X10=163,28, то подразумеваем величину
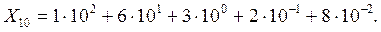
Нижний индекс в записи числа указывает на основание используемой системы счисления. В принципе, роль основания способно играть любое вещественное число. Переход от системы счисления с произвольным основанием к десятичной системе счисления осуществляется при помощи выражения 1.1, которое справедливо как для целой, так и для дробной частей числа. Возьмем, например, восьмеричное число 3678 и преобразуем его в десятичное. Вполне логично записать это число как
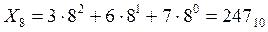 .
.
Переход от десятичной системы счисления к системе счисления с произвольным основанием выполняется в соответствии со следующими правилами: целая часть десятичного числа делится на основание новой системы счисления, запись целой части нового числа производится с последнего результата деления (старший разряд целой части); дробная часть десятичного числа умножается на основание новой системы счисления, запись результата нового числа производится с первого результата умножения (старший разряд дробной части).
То же самое десятичное число 24710 можно записать в виде 111101112 двоичного числа. Действительно
247:2=123+1 (X0=1)
123:2=61+1 (Х1=1)
61:2=30+1 (Х2=1)
30:2=15+0 (Х3=0)
15:2=7+1 (Х4=1)
7:2=3+1 (Х5=1)
3:2=1+1 (Х6=1)
1:2=0+1 (Х7=1)
Записываем число в новой системе счисления с последнего результата деления: 111101112.
Осуществим перевод дробного десятичного числа 125,4810 в двоичное. Переведем сначала целую часть:
125:2=62+1 (Х0=1)
62:2=31+0 (Х1=0)
31:2=15+1 (Х2=1)
15:2=7+1 (Х3=1)
7:2=3+1 (Х4=1)
3:2=1+1 (Х5=1)
1:2=0+1 (Х6=1)
Записываем целую часть: 12510=11111012.
Переведем теперь дробную часть:
0,48×2=0+0,96 (Х-1=0)
0,96×2=1+0,92 (Х-2=1)
0,92×2=1+0,84 (Х-3=1)
0,84×2=1+0,68 (Х-4=1)
0,68×2=1+0,36 (Х-5=1)
0,36×2=0+0,72 (Х-6=0)
0,72×2=1+0,44 (Х-7=1)
и т.д.
Следует иметь в виду, что дробная часть числа в новой системе счисления может иметь большое количество разрядов и даже оказаться бесконечной. Поэтому нет необходимости находить все разряды, а можно ограничиться лишь их частью исходя из требований точности представления числа. В нашем случае ограничимся семью разрядами дробной части и запишем ее с первого результата умножения 0,4810=0,01111012. Окончательно получается 125,4810=1111101,01111012.
Для представления числа с основанием системы счисления S средствами цифровой вычислительной техники необходимо, чтобы электронное устройство могло формировать на выходе и воспринимать на входе S различных состояний электрических сигналов. При этом каждый разряд должен обрабатываться своим отдельным узлом данного устройства. Поэтому, чем выше основание системы счисления, в которой представляются обрабатываемые числа, тем меньше требуется разрядов и, следовательно, узлов электронного устройства. С другой стороны, количество различных состояний электрических сигналов возрастает. Так для представления десятичных чисел средствами электронной техники необходимо, чтобы электронный узел был способен различать десять состояний (уровней напряжения или тока) электрического сигнала. Реализация такого устройства является достаточно сложной технической задачей. Кроме того, такое устройство будет помехонезащищенным из-за сложности идентификации одного из десяти параметров электрического сигнала, что повысит вероятность ошибочного результата обработки. Требования помехоустойчивости в вычислительных устройствах имеют больший приоритет перед аппаратными затратами и, поэтому, наибольшее распространение получила двоичная система счисления, оперирующая с двумя разрядными коэффициентами 0 и 1. Один разряд двоичного кода носит название бит. Группа разрядов из восьми бит называется байтом. Логическому нулю в цифровых вычислительных устройствах обычно соответствует электрический сигнал с низким уровнем напряжения (тока), а логической единице – с высоким.
Кроме двоичной в цифровых вычислительных устройствах часто применяются восьмеричная, шестнадцатеричная и десятичная системы счисления. В десятичной системе счисления осуществляется, как правило, ввод и вывод информации в цифровые вычислительные устройства с помощью специальных преобразователей с целью упрощения человеко-машинного взаимодействия. Восьмеричная и шестнадцатеричная системы счисления используются в основном из-за компактности записи чисел и удобства перевода двоичных кодов в восьми- и шестнадцатеричные. Для записи шестнадцатеричных чисел используются шестнадцать знаков - десять арабских цифр от 0 до 9 для записи первых десяти цифр и символы латинского алфавита от A до F для записи оставшихся шести цифр от 10 до 15 (A соответствует цифре 10, В- 11, C- 12, D- 13, E- 14, F- 15). Так, например, шестнадцатеричное число 4D16 соответствует десятичному числу 7710, так как 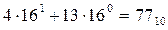 .
.
Достоинство восьмеричной и шестнадцатеричной форм записи числа – это легкость перевода из двоичной формы в восьмеричную (шестнадцатеричную) и наоборот. Так как 8=23 и 16=24, то для записи одного разряда восьмеричного числа требуются три разряда двоичного, а одного разряда шестнадцатеричного – четыре разряда двоичного. Например, чтобы перевести шестнадцатеричное число 1ED9,0A16 в двоичную форму, необходимо каждую шестнадцатеричную цифру представить эквивалентным четырехразрядным двоичным числом: 116=00012, E16=11102, D16=11012, 916=10012, 016=00002, A16=10102. В итоге, отбросив три незначащих нуля перед первой единицей, получим число 1111011011001,000010102.
Для ввода и вывода десятичной информации в цифровые вычислительные устройства обычно используется не сама десятичная система счисления, а двоично-десятичная, которая позволяет представить десятичные числа с использованием двоичных кодов. В этой форме каждая цифра десятичной записи числа изображается в виде четырехразрядного двоичного числа (двоичной тетрады). Таким образом, двоично-десятичная система счисления является как бы ограниченным до первых десяти символов вариантом шестнадцатеричной системы. Например, чтобы представить десятичное число 174,8310 в двоично-десятичной форме необходимо, как и в случае с шестнадцатеричной системой счисления, каждый разряд десятичного числа перевести в четырехразрядный двоичный код: 110=00012, 710=01112, 410=01002, 810=10002, 310=00112. Окончательно число будет иметь вид 000101110100,100000112-10. В записи двоично-десятичного числа незначащие нули принято оставлять, поскольку оно всегда является формой представления десятичного числа и обрабатывается по группам из четырех разрядов. В связи с этим, нельзя путать двоично-десятичную форму записи числа с двоичной записью того же числа. В первом случае основание системы счисления остается равным десяти - только разрядные коэффициенты при основании выражены в двоичной форме. Для удобства в таблице 1.1 приведены различные формы записи двадцати чисел натурального ряда.
Таблица 1.1.
| Десятичное число | Двоичное число | Восьмеричное число | Шестнадцате-ричное число | Двоично-десятичное число |
Продолжение таблицы 1.1.
| Десятичное число | Двоичное число | Восьмеричное число | Шестнадцате-ричное число | Двоично-десятичное число |
| A | ||||
| B | ||||
| C | ||||
| D | ||||
| E | ||||
| F | ||||
1-2. Числовые коды, представление отрицательных чисел.
Кодом называется любое обозначение, отличное от общепринятого. Общепринято, например, положительные числа отмечать знаком «+» (или вообще не указывать знак), а отрицательные числа отмечать знаком «-». Числа разного знака необходимо уметь изображать состояниями элементов цифровой электроники. Для изображения знака числа вводится дополнительный знаковый разряд, причем состоянию «0» этого разряда соответствует знак «+», а состоянию «1» - знак «-».Такое изображение чисел со знаком называется прямым кодом [X]пр числа Х. Поскольку разрядность цифровых вычислительных устройств обычно кратна одному байту, то под знаковый разряд отводится крайний левый бит в старшем байте. Таким образом, если для представления чисел в цифровом устройстве предусмотрен один байт (8 бит), то знаковым будет восьмой разряд байта, а оставшиеся семь будут отведены для значащих разрядов числа, что сделает возможным оперировать с целыми числами в диапазоне от –127 до +127. Если же разрядность цифрового устройства 2 байта (16 бит), то знаковым будет шестнадцатый разряд, а значащими окажутся разряды с первого по пятнадцатый и т.д. Таким образом, прямой код целого числа образуется по правилу: если число X положительно, то Xпр=0, X1, X2, ... Xn; если число X отрицательно, то Xпр=1, X1, X2, ... Xn, где n =8, 16 и т.д.
Обратный код числа образуется инвертированием всех разрядов прямого кода числа, кроме знакового. Операция инвертирования заключается в поразрядной замене нулей на единицы и единиц на нули. Таким образом, если число X положительно, то Xобр=0, 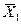 ,
, 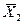 , ...
, ... 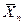 ; если число X отрицательно, то Xобр=1,
; если число X отрицательно, то Xобр=1, 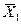 ,
, 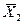 , ...
, ... 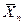 , где n = 8, 16 и т.д.
, где n = 8, 16 и т.д.
Как известно, правила сложения чисел отличаются от правил вычитания. Чтобы выполнить эти операции необходимо иметь два самостоятельных устройства - сумматор и вычитатель. Но оказалось, что можно обойтись только одним устройством - сумматором, если изображать числа, участвующие в операции, в дополнительных кодах. Дополнительный код положительного числа совпадает с прямым кодом этого числа.
Дополнительный код отрицательного числа получается следующим образом:
записывают обратный код исходного числа;
прибавляют единицу к младшему разряду.
Дополнительный код числа будем обозначать как Xдоп. При этом, если в результате вычитания в знаковом разряде получается единица, то результат отрицательный и представлен в дополнительном коде, а если нуль – то положительный и представлен в прямом коде. В таблице 1.2 приводится пример кодов некоторых положительных и отрицательных десятичных чисел.
Таблица 1.2.
| Десятичное представление | Двоичное представление | Представление в прямом коде [X]пр | Представление в обратном коде Xобр | Представление в дополнительном коде Xдоп |
| -1 | -1 | |||
| -17 | -10001 | |||
| -70 | -1000110 |
В процессе выполнения арифметических операций необходимо следить за тем, чтобы промежуточные и конечные результаты не выходили бы за пределы отведенной разрядной сетки. Для этих целей используют так называемый модифицированный дополнительный код 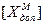 . Согласно этому коду под знаковый отводится не один, а два разряда. Правила перевода в модифицированный дополнительный код такие же, как и в обычный дополнительный код. Отличие состоит в том, что в модифицированном дополнительном коде положительному числу в знаковых разрядах соответствуют два нуля и отрицательному числу – две единицы. При этом, если в результате некоторой арифметической операции в знаковых разрядах произошло чередование нуля и единицы (возникли комбинации 01 или 10), то имело место переполнение разрядной сетки и результат следует считать неверным.
. Согласно этому коду под знаковый отводится не один, а два разряда. Правила перевода в модифицированный дополнительный код такие же, как и в обычный дополнительный код. Отличие состоит в том, что в модифицированном дополнительном коде положительному числу в знаковых разрядах соответствуют два нуля и отрицательному числу – две единицы. При этом, если в результате некоторой арифметической операции в знаковых разрядах произошло чередование нуля и единицы (возникли комбинации 01 или 10), то имело место переполнение разрядной сетки и результат следует считать неверным.
В принципе, логика выполнения арифметических операций в двоичной системе счисления наиболее проста. Это наглядно видно на примере сравнения таблиц умножения десятичных цифр с одной единственной таблицей умножения двоичных цифр, имеющей вид: 00=0; 01=0; 10=0; 11=1.
Необходимо особо подчеркнуть, что правила выполнения арифметических операций над многоразрядными числами, представленными в позиционных системах счисления с различными основаниями, одни и те же. Отличие составляют лишь правила сложения и умножения одноразрядных чисел (для каждой системы счисления - свои таблицы умножения и сложения).
В цифровых вычислительных устройствах для реализации операций быстрого деления и умножения числа на 2n, где n – целое положительное число, используются операции сдвига двоичного кода числа вправо или влево. Сдвинуть двоичный код влево на один разряд соответствует умножению его на 2, а вправо – делению на 2. Например, десятичному числу 8 соответствует двоичный код 00001000, а десятичному числу 16, равному удвоенному значению 8, двоичный код 00010000. Очевиден сдвиг кода влево на один разряд. Десятичному же числу 4, вдвое меньшему 8, соответствует двоичный код 00000100. Налицо сдвиг вправо на один разряд двоичного кода. При проектировании цифровых умножителей на произвольный коэффициент используется алгоритм традиционного умножения столбиком.
1-3. Определение функции алгебры логики.
Для анализа и синтеза цифровых электронных схем широко используется математический аппарат алгебры логики, или булевой алгебры, разработанной в середине XIX века ирландским математиком Дж. Булем. Основным понятием алгебры логики является понятие переключательной функции или булевой функции алгебры логики (ФАЛ). Функцией алгебры логики n переменных называется такая функция, которая принимает только два возможных значения - 0 или 1, как и переменные, от которых эта функция зависит. Для n переменных возможно 2n различных значений переключательной функции f. Если заданы все 2n значений функции, то она называется полностью определенной. Если же часть значений функции f не задана, то такая функция носит название неопределенной или частично определенной.
ФАЛ задаются таблично (в виде так называемых таблиц истинности), аналитически (в виде алгебраических выражений), в виде последовательности десятичных чисел или в виде кубических комплексов. В таблице 1.3 приведен пример табличного задания произвольной функции трех переменных f=f(A,B,C).
Таблица 1.3.
| j | A | B | C | F |
Конкретная комбинация значений аргументов носит название набора. Каждый набор имеет индекс j, численно равный десятичному эквиваленту двоичного числа.
ФАЛ от одной и двух переменных принято называть элементарными. Эти функции имеют специальные названия и обозначения и используются при воспроизведении более сложных логических функций. В таблице 1.4 приведены все возможные переключательные функции двух переменных.
Таблица 1.4.
| fj | X: | Название функции | Обозначение функции | ||||
| Y: | |||||||
| f0 | константа 0 | ||||||
| f1 | конъюнкция X и Y | XY; X&Y; XY | |||||
| f2 | функция запрета по Y | XY | |||||
| f3 | переменная X | X | |||||
| f4 | функция запрета по X | YX | |||||
| f5 | переменная Y | Y | |||||
| f6 | функция неравнозначности (сложение по модулю два) | XY | |||||
| f7 | дизъюнкция X и Y | XY, X+Y | |||||
| f8 | стрелка Пирса | XY | |||||
| f9 | функция равнозначности | XY | |||||
| f10 | инверсия Y | 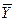
| |||||
| f11 | импликация от X к Y | XY | |||||
| f12 | инверсия X | 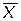
| |||||
| f13 | импликация от Y к X | YX | |||||
| f14 | штрих Шеффера | XY | |||||
| f15 | константа 1 |
Для аналитической записи переключательных функций используются вспомогательные функции, называемые конституентой единицы и конституентой нуля. Конституентой единицы n переменных называется такое булево произведение (конъюнкция) этих переменных, в которое каждая переменная входит только один раз в прямой или инверсной форме. Переменная, принимающая на данном наборе единичное значение, записывается в конституенте единицы в прямом виде, а отрицательное – в инверсном виде. Отличительной особенностью конституенты единицы является то, что она равна «1» только на одном, вполне определенном наборе значений переменных. Будем обозначать конституенту единицы символом mj, где индекс jуказывает на номер набора, на котором конституента единицы становится равной «1». Аналогично конституента нуля есть булево сложение (дизъюнкция) n логических переменных, которое обращается в «0» лишь при одном наборе аргументов. При этом в прямом виде в конституенте нуля будет записываться переменная, принимающая на данном наборе нулевое значение, а в инверсном – единичное значение.
Аналитическая запись функции осуществляется по таблице истинности. Непосредственно из данных таблицы находится так называемая совершенная дизъюнктивная нормальная форма булевой функции (СДНФ) по выражению:
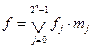 ,
,
где fj - значение функции на j-ом наборе, mj - конституента единицы, равная «1» только на одном j-ом наборе, Ú - символ логического сложения (дизъюнкции), аналогичный символу алгебраического сложения .
Для записи выражений в совершенной конъюктивной нормальной форме (СКНФ) используют формулу:
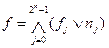 ,
,
где fj - значение функции на j-ом наборе, nj - конституента нуля, равная «0» только на одном j-ом наборе, Ù - символ логического произведения (конъюнкции), аналогичный символу алгебраического произведения Õ.
Проиллюстрируем СДНФ и СКНФ переключательной функции на примере булевой функции 3-х переменных, заданной таблицей 1.3. Формула для любой СДНФ функции 3-х переменных будет иметь вид:
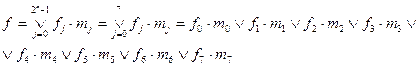
Подставляя из таблицы значения функций f0f7, получаем:
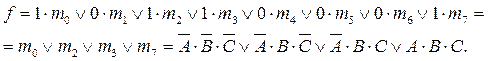
Формула для любой СКНФ функции 3-х переменных будет иметь вид:
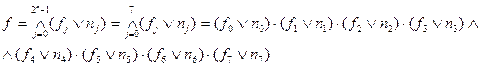
Подставляя из таблицы значения функций f0f7, получаем:
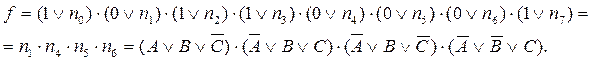
Аналогично находятся СДНФ и СКНФ любой другой булевой функции, заданной таблично.
Аналитическая запись ФАЛ, а также ее дальнейшие тождественные преобразования с целью получения оптимального вида опираются на следующие основные законы и тождества алгебры логики:
- переместительный закон XY=YX, XY=YX;
- сочетательный закон X(YZ)=(XY)Z, X(YZ)=(XY)Z;
- распределительный закон X(YZ)=XYXZ, XYZ=(XZ)(YZ);
- закон отрицания (правило де Моргана) 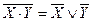 ,
, 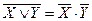 ;
;
- закон двойного отрицания 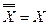 ;
;
- закон идемпотентности XX=X, 1X=1, 0X=X,
XX=X, 1X=X, 0X=0;
- закон склеивания X 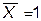 ,
, 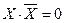 ;
;
- закон поглощения YXX=X; (YX)X=X;
- константы 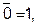
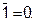
Иногда вместо аналитической формы используют запись логической функции в виде последовательностей десятичных чисел. Такая запись является аналогом таблиц истинности и СДНФ или СКНФ, но при этом является гораздо более компактной. При этом в скобках указывают десятичные эквиваленты двоичных кодов конституент единицы или нуля, или, что одно и то же, номера наборов функции f, в которых она принимает единичные или нулевые значения. При указании номеров наборов с единичными значениями функции перед скобкой слева указывается знак дизъюнкции 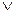 или
или 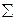 , а с нулевыми – знак конъюнкции
, а с нулевыми – знак конъюнкции 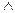 или
или 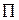 . В качестве примера запишем функцию, заданную таблицей 1.3 в виде десятичных чисел на единичных и нулевых наборах:
. В качестве примера запишем функцию, заданную таблицей 1.3 в виде десятичных чисел на единичных и нулевых наборах:
f(A,B,C)= 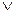 (0,2,3,7)=
(0,2,3,7)= 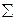 (0,2,3,7);
(0,2,3,7);
f(A,B,C)= 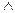 (1,4,5,6)=
(1,4,5,6)= 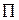 (1,4,5,6).
(1,4,5,6).
В случае автоматизированного проектирования логических схем электронных цифровых устройств на ЭВМ ФАЛ удобно записывать в виде кубических комплексов. Такая форма в силу ограниченного числа символов позволяет формализовать запись логических функций большого числа переменных. Каждый набор переменных представляется в виде n-мерного вектора, где n – количество входных переменных. Вершины этого вектора образуют вершины n-мерного куба. Если функция задана тремя переменными, то она образует трехмерный куб, который легко представляется геометрически в виде объемной фигуры. Все единичные вершины куба, в которых функция f принимает значение «1», образуют множество нулевых кубов, называемое нулевым кубическим комплексом К0. Нулевой кубический комплекс записывается набором двоичных кодов входных переменных, для которых функция принимает единичные значения. Вершины, расположенные на концах ребер куба, называются соседними и отличаются только одной переменной. Если два куба, для которых функция равна «1», являются соседними, то они образуют куб более высокого порядка. Так, если два нулевых куба комплекса К0 являются соседними, т.е. отличаются только одной переменной, то они образуют единичный куб, геометрически представляющий ребро исходного n-мерного куба. Набор единичных кубов образуют единичный кубический комплекс К1. Записывается единичный кубический комплекс в виде набора двоичных кодов совпадающих переменных, а вместо несовпадающих проставляются прочерки. Аналогично соседние единичные кубы, отличающиеся только одной переменной, образуют двоичные кубы, набор которых в свою очередь образуют двоичный кубический комплекс К2 и т.д.
Рассмотрим запись ФАЛ в виде кубических комплексов на примере функции, заданной таблицей 1.3. Поскольку функция определяется тремя переменными, то ее можно представить трехмерным кубом (рис. 1.1). Вершины этого куба сформированы таким образом, чтобы каждая переменная, входящая в уравнение, располагалась в одной оси базиса трехмерного пространства X-Y-Z. В оси Х располагается переменная А, в оси Y – переменная В и в оси Z – переменная С. Окружностями отмечаем вершины куба, в которых функция принимает значения единицы. Эти вершины (нулевые кубы) образуют нулевой кубический комплекс К0=(000, 010, 011, 111). Из рисунка наглядно видны соседние вершины, в которых нулевые кубы отличаются только одной переменной. Ребро исходного куба, образованное соседними вершинами, выделяем толстой линией. Эти ребра образуют единичные кубы, в записи которых вместо несовпадающих переменных ставятся прочерки. Набор единичных кубов образует единичный кубический комплекс К1=(0-0, 01-, -11).
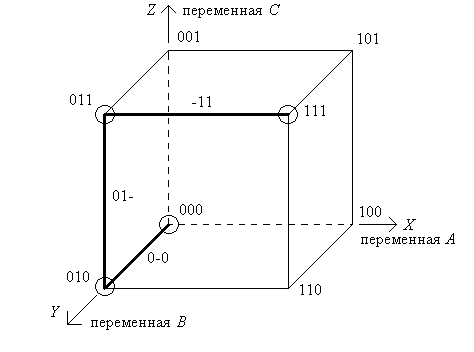
Рис. 1.1. Кубические комплексы функции, заданной таблицей 1.3.
Единичный кубический комплекс для рассмотренного выше примера является максимально возможным. Для некоторых произвольных функций трех переменных может оказаться возможным выделение двоичных кубов, образующих двоичный кубический комплекс К2. Геометрически такие кубы образовывают грани исходного трехмерного куба. В записи двоичных кубов будет присутствовать значение одной совпадающей переменной и два прочерка для несовпадающих, например, (-1-). Для функции n переменных существует теоретическая вероятность нахождения (n-1) кубических комплексов. Совокупность всех кубических комплексов образует кубический комплекс ФАЛ: К(f)= 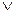 (К0, К1, …, Кm), где m – максимально возможный кубический комплекс функции n переменных.
(К0, К1, …, Кm), где m – максимально возможный кубический комплекс функции n переменных.
Для выражения ФАЛ от многих переменных достаточно иметь ограниченное число разнотипных элементарных переключательных функций, называемое системой. Как показано выше, любая функция алгебры логики может быть записана в виде СДНФ или СКНФ. Следовательно, любую функцию аргументов можно представить с помощью системы только из трех элементарных функций: инверсия, дизъюнкции и конъюнкции.
Система функций алгебры логики называется функционально полной, если любая функция от произвольного числа аргументов n может быть представлена с помощью этих функций. Полная система функций называется базисом. Минимальным базисом называется такой базис, для которого удаление хотя бы одной из функций, образующих этот базис, превращает систему функций в неполную. Так, полная система из дизъюнкции, конъюнкции и инверсии может быть сокращена, поскольку с помощью формул де Моргана можно представить либо конъюнкцию через инверсию и дизъюнкцию, либо дизъюнкцию через инверсию и конъюнкцию. Таким образом, базис из дизъюнкции, конъюнкции и инверсии не является минимальным. Поскольку ни дизъюнкция, ни конъюнкция не могут быть выражены через инверсию и наоборот, то базисы, состоящие из инверсии и дизъюнкции и из инверсии и конъюнкции, являются минимальными.
Возможны различные базисы и минимальные базисы, отличающиеся числом входящих в них функций и их видом. Приведем примеры функционально полных систем:
- конъюнкция, дизъюнкция, инверсия;
- конъюнкция, инверсия;
- дизъюнкция, инверсия;
- стрелка Пирса;
- штрих Шеффера.
Выбор минимального базиса связан с выбором стандартного набора логических элементов, из которых будет строиться конкретное цифровое устройство. Очевидно, что уменьшение числа функций, входящих в базис, соответствует уменьшению числа различных логических элементов, принятых за стандартные. Однако уменьшение типов стандартных элементов может привести к увеличению их общего числа. Таким образом, сложность цифрового устройства зависит не только от вида реализуемой функции, но и от вида функций, выбранных в качестве базиса.
1-4. Минимизация функций алгебры логики.
Переключательные функции являются математическими моделями некоторых реальных электронных цифровых схем. Для того чтобы синтезировать наиболее оптимальное цифровое устройство (например, имеющее минимальные аппаратные затраты), математическую модель этого устройства, представленную в виде СДНФ или СКНФ, преобразуют к соответствующему виду с использованием приведенных выше законов алгебры логики. Преобразование СДНФ или СКНФ логической функции к минимальному виду аналитической записи называется процессом минимизации ФАЛ. Однако результат минимизации функции с помощью законов и тождественных преобразований булевой алгебры во многом зависит от опыта разработчика и не всегда является очевидным. Поэтому разработан ряд алгоритмов, формализующих и автоматизирующих подобные преобразования.
Рассмотрим один из алгоритмов минимизации, предложенный американский ученым Вейчем. Вейч предложил специальные диаграммы-карты, в которые можно записать все конституенты единицы, входящие в СДНФ (конституенты нуля, входящие в СКНФ) той или иной булевой функции. На рис. 1.2 в качестве примера приведены диаграммы для минимизаций функций двух, трех и четырех переменных соответственно.
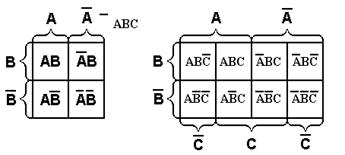
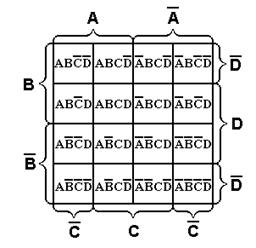
Рис. 1.2. Диаграммы Вейча для функций 2-х, 3-х и 4-х переменных.
Каждой клетке диаграммы в случае минимизации СДНФ соответствует определенная конситуента единицы. Метод минимизации с помощью диаграмм Вейча заключается в следующем. Конституенты единицы, входящие в СДНФ булевой функции, заносятся в соответствующие клетки диаграммы. Удобно наличие соответствующей конституенты единицы изображать в клетке диаграммы цифрой 1, а отсутствие - 0. Все диаграммы построены таким образом, что рядом расположенные единицы по горизонтали или вертикали склеиваются между собой в соответствии с законом склеивания алгебры логики. Одну и ту же конституенту единицы можно использовать для склеивания с несколькими другими конституентами единицы с целью получения наиболее простого окончательного выражения. Цель всех операций - получить как можно меньшее число прямоугольников (в том числе квадратов), чтобы число членов СДНФ уменьшилось, получив в итоге МДНФ.
Формировать прямоугольники можно только при включении в них хотя бы одного нового члена. Склеивание можно осуществлять и путем замыкания крайних ребер в «бочку». Таким образом, полученная диаграмма Вейча геометрически образует цилиндр. На рис. 1.3 приведены некоторые правила склеивания конституент единицы для функций 2-х и 3-х переменных.
Поскольку для ФАЛ трех переменных диаграмма представляет как бы развертку цилиндра, разрезанного по 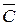 , поэтому единицы, расположенные по краям диаграммы (например, как это изображено на рис. 1.3) считаются расположенными рядом.
, поэтому единицы, расположенные по краям диаграммы (например, как это изображено на рис. 1.3) считаются расположенными рядом.
Метод минимизации СДНФ с помощью диаграмм Вейча включает в себя следующие шаги:
1. производится занесение в соответствующую диаграмму конституент единицы, входящих в СДНФ минимизируемой функции;
2. используя приведенные выше правила склеивания, находят простые импликанты функций (простой импликантой называется некоторая конъюнкция, полученная в результате склеивания конституент единицы, не участвующая в склеивании ни с одной другой из конъюнкций);
3. находится искомая минимальная дизъюнктивная нормальная форма (МДНФ) ФАЛ выбором минимальной совокупности простых импликант, покрывающей все конституенты единицы диаграммы.
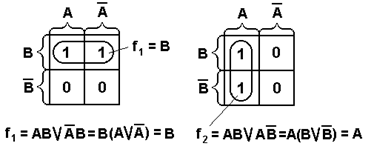
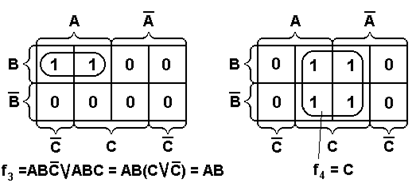
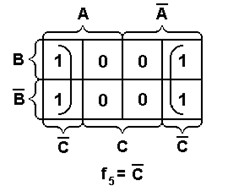
Рис. 1.3. Примеры для иллюстрации правил склеивания.
В качестве примера найде
Дата добавления: 2022-02-05; просмотров: 476;











