Дешифраторы и шифраторы.

Дешифратор – это устройство, предназначенное для преобразования двоичного кода в напряжение логической единицы (логического нуля) на том выходе, номер которого совпадает со значением двоичного кода на входе. Иными словами дешифратор преобразует двоичный код в унитарный. Унитарным называется код, в котором единица присутствует только в одном разряде, а в остальных - нули. При n входах в полном дешифраторе имеется m=2ⁿ выходов, т.е. для каждой комбинации входных сигналов имеется соответствующий выход. Дешифратор, у которого при n входах число выходов меньше чем 2ⁿ, называется неполным. Другое название дешифратора - декодер. Часто количество входов и выходов дешифратора формулируют записью «из n в m». Принцип работы полного трехразрядного дешифратора рассмотрим на примере его таблицы истинности (таблица 8.4). Обычно выходы дешифратора реализуют в инверсном виде. В скобках в таблице для такого случая указаны инверсные значения выходных функций.

Таблица 8.4

Входы	Выходы
X3	X2	X1
			0 (1)	0 (1)	0 (1)	0 (1)	0 (1)	0 (1)	0 (1)	1 (0)
			0 (1)	0 (1)	0 (1)	0 (1)	0 (1)	0 (1)	1 (0)	0 (1)
			0 (1)	0 (1)	0 (1)	0 (1)	0 (1)	1 (0)	0 (1)	0 (1)
			0 (1)	0 (1)	0 (1)	0 (1)	1 (0)	0 (1)	0 (1)	0 (1)
			0 (1)	0 (1)	0 (1)	1 (0)	0 (1)	0 (1)	0 (1)	0 (1)
			0 (1)	0 (1)	1 (0)	0 (1)	0 (1)	0 (1)	0 (1)	0 (1)
			0 (1)	1 (0)	0 (1)	0 (1)	0 (1)	0 (1)	0 (1)	0 (1)
			1 (0)	0 (1)	0 (1)	0 (1)	0 (1)	0 (1)	0 (1)	0 (1)

Соответствующие таблице истинности ФАЛ для прямых и инверсных значений выходных функций соответственно имеют вид

.

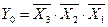
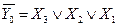
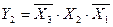
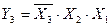
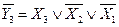
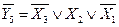
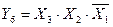
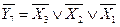Функциональная схема трехразрядного дешифратора, синтезированная на основе полученных ФАЛ для прямых значений выходных функций приведена на рис. 8.7,а, а для инверсных - на рис. 8.7,б.

Условные графические обозначения дешифратора «из 3 в 8» в электрических функциональных и принципиальных схемах приведены на рис.8.8. Часто для обозначений входов и выходов в дополнительном поле УГО микросхемы проставляют весовые или разрядные коэффициенты соответствующих систем счисления. Т.е. для трех двоичных входов дешифратора такие весовые коэффициенты будут иметь обозначения «1», «2» и «4», а для семи выходов унитарного кода - соответствующие разрядные коэффициенты десятичной системы счисления «0», «1», …, «7».

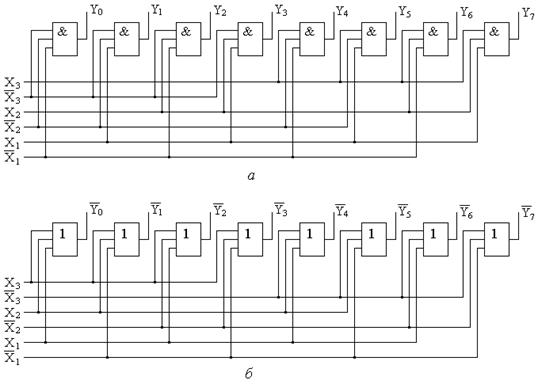
Рис. 8.7. Функциональная схема трехразрядного дешифратора с прямыми (а) и инверсными (б) выходами.

Рис. 8.8. Условное графическое обозначение дешифратора «из 3 в 8» на функциональных (а) и принципиальных (б) схемах.

В общем случае логические уравнения для прямых и инверсных значений выходных переменных дешифратора на n входов имеют вид

……… ………

.

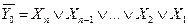
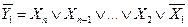
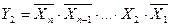
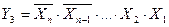
Построенные по полученным формулам дешифраторы с использованием n-входовых элементов И или ИЛИ называются линейными. К преимуществу линейных дешифраторов можно отнести высокое быстродействие, поскольку входные переменные одновременно поступают на все элементы. Одновременно, без дополнительных задержек, формируется и результат на выходах этих элементов. В существующих микросхемах элементов И и ИЛИ количество входов ограничено обычно восемью. Следовательно, ограничена и разрядность реализуемых на их основе линейных дешифраторов, что является недостатком.

Указанного недостатка лишены пирамидальные дешифраторы или, как их еще называют, многоступенчатые. Принцип построения этих дешифраторов состоит в применении только двухвходовых элементов. Сначала строят линейный дешифратор первой ступени для двухразрядного числа X₁, X₂ из четырех двухвходвых элементов И, как это показано на рис 8.9. Затем полученные конъюнкции объединяют элементами И с переменной X₃ в прямом и инверсном видах, образуя вторую ступень дешифратора. Наращивая таким образом структуру, можно построить пирамидальный дешифратор на произвольное число входов. Для этого каждая следующая ступень должна содержать в два раза большее количество двухвходовых элементов по сравнению с предыдущей. Общее количество ступеней должно быть на единицу меньшим, чем разрядность входного двоичного кода.

Для пирамидальных дешифраторов n-разрядного слова требуется большее количество двухвходовых логических элементов, чем для линейных дешифраторов такой же разрядности n-входовых. Однако следует иметь в виду, что количество логических элементов, располагаемых в одном корпусе ИС, определяется главным образом требуемым количеством выводов. Следовательно, в одном корпусе ИС можно расположить большее число двухвходовых элементов, чем трехвходовых, четырехвходовых и т.д. И значит, пирамидальная структура дешифратора по числу корпусов ИС может оказаться более предпочтительной, чем линейная. Это уже справедливо для дешифратора «из 4 в 16». Для линейной схемы необходимо было бы использовать шестнадцать четырехвходовых элементов И. Учитывая, что одна микросхема содержит два четырехвходовых элемента И, общее количество микросхем составило бы восемь штук. Для пирамидальной структуры потребовалось бы 4+8+16=28 двухвходовых элемента И. Так как в одном корпусе микросхемы содержится четыре двухвходовых элемента, то общее количество корпусов в этом случае составит 7 штук.

Рис. 8.9. Функциональная схема пирамидального дешифратора «из 3 в 8».

Дальнейшим развитием пирамидального дешифратора является матричный дешифратор. В структуре матричного дешифратора входной двоичный код разбивается на две группы по n и m разрядов. Коды обоих групп дешифрируются двумя независимыми дешифраторами. Выходные цепи этих дешифраторов объединяются в матрицу размерностью nхm, например, как это показано на рис.8.10. В пересечениях строк и столбцов матрицы устанавливаются схемы совпадения единиц (двухвходовые элементы И), формируя унитарный выходной код разрядностью из декодированных унитарных кодов соответствующих групп разрядов n и m. Если используются дешифраторы на одинаковое количество разрядов n=m, то матрица элементов И будет квадратной, в противном случае – прямоугольной.

Рис.8.10. Функциональная схема матричного дешифратора «из 4 в 16».

Существующие микросхемы дешифраторов кроме информационных входов подачи двоичного кода имеют обычно управляющий вход разрешения E - enable (разрешить). При подаче на этот вход активного уровня сигнала дешифратор работает в соответствии с рассмотренными правилами. При подаче на данный вход пассивного уровня сигнала, на всех выходах дешифратора устанавливаются логические нули. Такой вход позволяется повышать разрядность дешифрируемого кода путем включения нескольких микросхем в каскадную структуру. На рис.8.11 показан пример каскадирования дешифраторов «из 2 в 4» в структуру «из 4 в 16». При логическом нуле в разряде X₄ через инвертор на разрешающий вход E верхнего дешифратора подается логическая единица, в результате формируется унитарный код на выходах верхнего дешифратора Y₀…Y₇. На вход E нижнего дешифратора в это время подается логический ноль, что соответствует нулям на выходах этого дешифратора. При подаче логической единицы в разряде X₄ дешифрация кода X₁, X₂, X₃ осуществляется нижним дешифратором, а на выходах верхнего устанавливаются логические нули. В результате формируются разряды Y₈…Y₁₅ выходного унитарного кода.

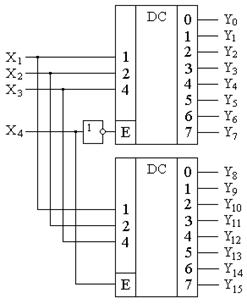
Рис.8.11. Функциональная схема каскадирования дешифраторов «из 3 в 8» в структуру «из 4 в 16».

Шифраторы выполняют задачу обратную той, которую выполняют дешифраторы: появление логической единицы (логического нуля) на определенном входе из m входов приводит к появлению соответствующей кодовой комбинации на n выходах. Также как и дешифраторы, шифраторы бывают полными и неполными. Число выходов полного шифратора определяется как . В общем случае количество входов и выходов дешифратора формулируют записью «из m в n». Работа восьмивходового полного шифратора с прямыми входами и выходами задается таблицей истинности (таблица 8.5).

Таблица 8.5

На основании таблицы истинности можно записать ФАЛ для прямых значений входных и выходных переменных, а также, используя свойство эквивалентности операций И и ИЛИ в прямой и инверсной логике (запись эквивалентна записи ), для инверсных значений входных и выходных переменных:

.

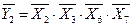
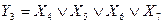
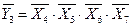Синтезированная на основании приведенных логических уравнений схема шифратора для прямых и инверсных входов и выходов представлена на рис.8.12.

Рис.8.12. Функциональная схема шифратора «из 8 в 3» с прямыми (а) и инверсными (б) входами и выходами.

Условные графические обозначения шифратора «из 8 в 3» в электрических функциональных и принципиальных схемах приведены на рис.8.13.

Рис. 8.13. Условное графическое обозначение шифратора «из 8 в 3» на функциональных (а) и принципиальных (б) схемах.

Существующие микросхемы шифраторов работают по несколько иному принципу, чем тот, который определен таблицей 8.5. Этой таблицей не определена ситуация, когда на входы шифратора подается сразу несколько единиц. Например, если на изображенной на рис 8.12,а схеме шифратора подать логические единицы на входы X₄ и X₂ одновременно, логические единицы появятся на выходах Y₃ и Y₂. Такая кодовая комбинация на выходе является нарушением работы шифратора, поскольку определяет подачу единицы на вход X₆, что не соответствует действительности. В реальных микросхемах реализуются так называемые приоритетные шифраторы. В таких шифраторах предусматривается одновременная подача активных уровней сигнала на несколько входов одновременно. Причем на выходах формируется двоичный код входа с максимальным номером, на который подан активный уровень сигнала. Также микросхемы шифраторов имеют дополнительные выводы, позволяющие наращивать разрядность шифруемого унитарного кода путем каскадного соединения нескольких микросхем. В качестве примера приведем микросхему приоритетного шифратора К555ИВ1, условное графическое обозначение которой приводится на рис.8.14, а логика работы определяется таблицей истинности 8.6. Крестиками в таблице обозначаются неопределенные значения, которые могут быть равны как единице, так и нулю.

Рис.8.14. Условное графическое обозначение шифратора К555ИВ1.

Таблица 8.6

Входы

Выходы

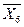
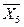
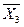
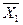
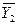
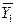
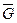
х

х

х

х

х

х

х

х

х

х

х

х

х

х

х

х

х

х

х

х

х

х

х

х

х

х

х

х

х

х

х

х

х

х

х

х

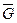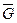Все выводы микросхемы К555ИВ1 инверсные. Кроме информационных выводов, микросхема также имеет управляющие выводы , и . Вывод выполняет функцию входа разрешения, – выхода переноса и – выхода признака подачи сигнала. При логической единице на входе работа микросхемы запрещена и на всех пяти выходах микросхемы установятся логические единицы. Разрешением работы микросхемы является логический ноль на входе . На выходе 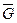формируется логический ноль, если хотя бы на один из информационных входов микросхемы подается активный логический ноль. Если на всех входах присутствуют пассивные логические единицы, на выходе 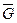устанавливается логическая единица, свидетельствующая об отсутствии воздействия на входы . На выходе переноса при всех единицах на входах и разрешающем нуле на входе будет установлен логический ноль, свидетельствующий о том, что дешифрация разрешена, но активный сигнал унитарного входного кода поступает на микросхему другой группы разрядов. Пример каскадного включения микросхем К555ИВ1 с целью синтеза шифратора «из 16 в 4» приведен на рис.8.15.

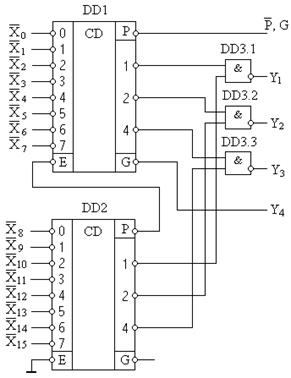
Рис.8.15. Пример каскадного включения микросхемы К555ИВ1 для синтеза приоритетного шифратора «из 16 в 4»

Выходы двоичного кода Y₁…Y₄ в такой схеме будут прямыми. Если логический ноль подан на один из входов , на выходах микросхемы DD3 появятся разряды Y₁, Y₂, Y₃ прямого выходного кода, на выходе 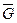DD1 – логический ноль, определяющий разряд Y₄ прямого выходного кода. Если логический ноль подается на один из входов , логическая единица с выхода запретит работу микросхемы DD1, а на выходах DD3 установятся значения разрядов Y₁, Y₂, Y₃ прямого выходного кода. В разряде Y₄ также установится логическая единица. Выход с микросхемы DD1 в такой схеме будет иметь смысл прямого выхода подачи активного входного сигнала хотя бы на один из входов, либо инверсного выхода переноса.

Шифраторы используются для построения устройств ввода первичной информации – клавиатур. Для этого необходимо активные уровни сигнала унитарного входного кода формировать с помощью ключей-кнопок клавиатуры. Аналогично можно реализовывать устроайства вывода информации с использованием дешифраторов, например индикаторы или исполнительные механизмы. На рис. 8.16 показан пример построения линейной и матричной клавиатур на 8 и 64 клавиш соответственно.

Рис.8.16. Пример реализации линейной клавиатура на базе шифратора (а) и матричной клавиатуры на базе шифратора и дешифратора (б).

В схеме рис.8.16,а входной логический ноль формируется путем нажатия соответствующей кнопки и замыкания входной цепи на нулевой потенциал общего провода. При отсутствии воздействия на кнопки входные потенциалы шифратора через резисторы R₁…R₈ подтянуты к напряжению питания, т.е. имеют пассивные уровни логических единиц. Соотвтетствующий двоичный код номера нажатой кнопки с выхода шифратора поступает в цифровую часть схемы измерительного устройства для последующей обработки. Признаком того, что хотя бы одна из кнопок нажата, является активный уровень сигнала «кнопка нажата», сформированный выводом G микросхемы шифратора. Этот сигнал может служить командой цифровому устройству, к которому подключена клавиатура, на то, чтобы оно приступило к считыванию кода нажатой кнопки. Такой сигнал может быть подан, например, на линию прерывания микропроцессорной системы (о прерываниях в микропроцессорных системах будет сказано в главе 12).

Линейные клавиатуры имеют ограничения по количеству кнопок, определяемые разрядностью шифратора. Поскольку многие современные измерительные устройства имеют широкую функциональность и могут требовать наличия большого количества управляемых органов, линейная организации в таком случае может оказаться недостаточной. Когда требуется формировать клавиатуры с большим количеством кнопок, конструктивно и схемотехнически оптимальной является матричная организация, пример которой показан на рис.8.16,б. В такой схеме кнопки SA1…SA64 устанавливаются в пересечениях строк и столбцов прямоугольной матрицы размерностью 8х8. Опрос кнопок осуществляется путем сканирования их в матрице. Цифровое устройство вырабатывает двоичный код, который преобразуется дешифратором DD2 (дешифратор в схеме изображен в зеркальном отображении, т.е. его входы в УГО показаны справа, а выходы слева) в унитарный инверсный код, в результате чего выбранный столбец матрицы приобретает потенциал уровня логического нуля. Это эквивалентно подключению к земле одного из контактов кнопок SA1…SA8 в схеме рис.8.16,а. Далее, если в выбранном столбце нажата кнопка, то на выходе шифратора DD1 сформируется ее двоичный код, а также станет активным сигнал «кнопка нажата». В противном случае сигнал «кнопка нажата» будет иметь пассивный уровень. С определенной периодичностью цифровое устройство будет менять двоичный код активизируемого столбца матрицы, в результате чего циклически будет производиться опрос всех столбцов. Таким образом, двоичный код активизируемого столбца будет выходным для цифрового устройства, к которому данная клавиатура подключена, а код номера кнопки в столбце – входным. При такой организации от цифрового устройства требуется, чтобы оно постоянно опрашивало клавиатуру, формируя двоичный код столбца на дешифратор столбцов. Часто подобным цифровым устройством является микропроцессорная система. Возложение на нее задачи постоянного формирования и чередования кодов столбцов матрицы приводит ее к загрузке этим процессом, что снижает производительность системы. Поэтому для разгрузки микропроцессорной системы в схеме клавиатуры используют устройство, автономно формирующее и чередующее коды столбцов матрицы. Таким устройством является счетчик DD3, на входы которого подается последовательность импульсов с генератора импульсов GN. В схеме подключение счетчика к входам дешифратора показано пунктирными линиями. Подробно о счетчиках будет сказано в главе 9. В общем случае счетчик формирует на выходе двоичный код количества импульсов, поступающих на его вход. Таким образом, код с выхода счетчика будет постоянно увеличиваться на единицу, что повлечет за собой активизацию соседних столбцов в матрице. Этот же код будет поступать в цифровое устройство уже как входной код для идентификации им номера активного столбца матрицы. Признаком того, что хотя бы одна кнопка нажата, будет наличие на выходе «кнопка нажата» активного уровня сигнала, являющегося для цифрового устройства командой на считывания кодов номеров столбца и нажатой кнопки в столбце.