Цифровые компараторы.
Цифровой компаратор предназначен для сравнения двух n-разрядных двоичных чисел A={a1, a2, ..., an} и B={b1, b2, ..., bn}. В результате сравнения может установливаться одно из соотношений: =, ≠; >; <; ≥; ≤. Выходная функция F принимает единичное значение, если проверяемое соотношение выполняется или нулевое – если не выполняется. Цифровой компаратор позволяет реализовывать ту часть алгоритма измерения в цифровой измерительной технике, в которой заложена процедура сравнения неизвестного значения измеряемой величины с цифровой мерой. Рассмотрим синтез компаратора для реализации функции равенства двух n-разрядных двоичных кодов. Факты равенства, больше и меньше отдельных разрядов определим функциями f(A=B)i, f(A>B)i и f(A<B)i, заданной следующей таблицей истинности 8.9:
Таблица 8.9.
| Входы | Выходы | |||
| ai | bi | f(A=B)i | f(A>B)i | f(A<B)i |
Тогда факт неравенства разрядов будет определяться инверсным значением функции 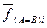 . Определим ФАЛ для f(A=B)i, соответствующую приведенной таблице истинности
. Определим ФАЛ для f(A=B)i, соответствующую приведенной таблице истинности
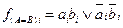 .
.
Синтезированная структурная схема в соответствии с формулой для f(A=B)i имеет вид, представленный рис. 8.22.
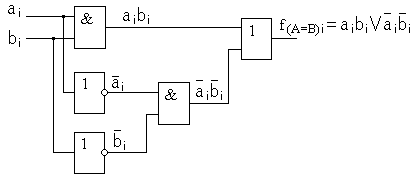
Рис. 8.22. Функциональная схема устройства сравнения одноразрядных кодов.
Выполним следующие преобразования над функцией f(A=B)i, используя тождества алгебры логики:
 ,
,
т.е. окончательно имеем инверсию функции исключающее ИЛИ.
Функция неравенства одного разряда 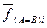 тогда будет выражаться через прямое значение функции Исключающее ИЛИ. Для перехода от равенства (неравенства) отдельных разрядов к функции равенства F(A=B) (неравенства
тогда будет выражаться через прямое значение функции Исключающее ИЛИ. Для перехода от равенства (неравенства) отдельных разрядов к функции равенства F(A=B) (неравенства  ) всего n-разрядного кода необходимо установить факт наличия логических единиц во всех функциях f(A=B)i (
) всего n-разрядного кода необходимо установить факт наличия логических единиц во всех функциях f(A=B)i ( 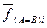 ). Это осуществляется n-входовым элементом И. ФАЛ для функции F(A=B) с учетом использования функции инверсии исключающего ИЛИ имеет вид
). Это осуществляется n-входовым элементом И. ФАЛ для функции F(A=B) с учетом использования функции инверсии исключающего ИЛИ имеет вид
 .
.
Функция f(A>B)i одноразрядного числа согласно таблице 8.9 будет реализовываться двухвходовым элементом И, на один вход которого будет подаваться разряд ai в прямом виде, а на второй – разряд 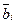 в инверсном виде, т.е.
в инверсном виде, т.е. 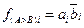 . Несколько сложнее обстоит дело со схемой сравнения n-разрядных слов на «больше». Для этого анализ неравенства должен выполняться последовательно в направлении от старших разрядов в сторону младших. Младшие разряды сравниваются при условии равенства старших. Тогда логика сравнения на «больше» для двухразрядного слова с учетом равенства/неравенства старшего разряда может быть представлена в следующем виде
. Несколько сложнее обстоит дело со схемой сравнения n-разрядных слов на «больше». Для этого анализ неравенства должен выполняться последовательно в направлении от старших разрядов в сторону младших. Младшие разряды сравниваются при условии равенства старших. Тогда логика сравнения на «больше» для двухразрядного слова с учетом равенства/неравенства старшего разряда может быть представлена в следующем виде
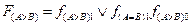 .
.
Аналогично можно записать логику сравнения для трехразрядного числа
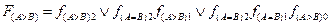
и четырехразрядного числа
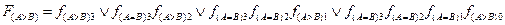 .
.
В общем случае функция сравнения на «больше» для произвольного n-разрядного числа можно выразить
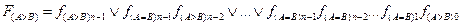
Подставив минтермы функций f(A>B)i в переменных ai и bi и эквивалентные функциям f(A=B)i элементы исключающее ИЛИ-НЕ, можно реализовать представленную ФАЛ для F(A>B).
Функцию сравнения на «меньше» можно определить как
 ,
,
т.е. только если будет отсутствовать факт равенства F(A=B)=0 и факт больше F(A>B)=0, то схемой совпадения нулей (функцией ИЛИ) установится общий ноль, а инверсия этого нуля даст единичное значение функции F(A<B) как последнего оставшегося варианта сравнения.
Пример схемы, реализующей рассмотренные выше функции F(A=B), F(A>B) и F(A<B) двух четырехразрядных чисел приведен на рис.8.23.

Рис.8.23. Функциональная схема компаратора, реализующего функции «равно», «больше», «меньше» двух четырехразрядных чисел.
Из-за громоздкости структуры компараторов чисел большой разрядности и необходимости использования в этом случае логических элементов с большим количеством входов, в интегральном исполнении обычно реализуются компараторы, сравнивающие двоичные коды с разрядностью n не более 4 или 8 бит. Для повышения разрядности обрабатываемых кодов сравниваемые слова разбиваются на группы фиксированной разрядности с индивидуальными выходами функций сравнения на «равно» F(A=B)i и «больше» F(A>B)i в каждой группе. Тогда описанный выше метод применим и для анализа n-разрядных кодов. Для этого выходы функций равенства и больше компараторов отдельных групп объединяются в часть схемы рис.8.23, заключенную в пунктирную линию. В результате формируется результат сравнения кодов всей длины. В условном графическом обозначении функция компаратора задается символами «= =» или «COMP».
В качества примера можно привести микросхему четырехразрядного компаратора К561ИП2, реализующую функции сравнения на «больше», «меньше» и «равно». Эта микросхема может также применяться для сравнения кодов большей разрядности (рис.8.24). Для этого в ней предусмотрены входы переноса функций «меньше» и «равно», на которые подаются выходы одноименных функций группы младших разрядов. Вход «больше» в данной микросхеме избыточен, и на него в микросхемах всех групп необходимо постоянно подавать потенциал логической единицы. На вход «меньше» микросхемы самой младшей группы необходимо подать логический ноль, а на вход «равно» - логическую единицу. Такое же включение микросхемы должно быть и при использовании ее для сравнения четырехразрядных слов.

Рис.8.24. Включение микросхемы К561ИП2 при повышения разрядности сравниваемых слов.
Сумматоры.
Сумматоры – это класс КЦУ, выполняющих операцию арифметического сложения двух двоичных n-разрядных чисел. Сумматоры бывают полными и неполными. Неполный сумматор или полусумматор для случая одноразрядного устройства - это комбинационное устройство с двумя входами и двумя выходами, выполняющее операцию сложения двух одноразрядных чисел в соответствии с таблицей истинности 8.10, где А и В – входные одноразрядные числа, Sп/см. – выход суммы, а Pп/см. – выход переноса в старший разряд:
Таблица 8.10
| Входы | Выходы | ||
| А | В | Sп/см. | Pп/см. |
Записанные по таблице ФАЛ для переменных Sп/см. и Pп/см. имеют вид
 ,
,
 .
.
Первое уравнение для Sп/см. обозначает операцию «Исключающее ИЛИ», а второе - для Pп/см. – операцию логической конъюнкции. Поскольку в большинстве серий микросхем имеются элементы «Исключающее ИЛИ», то схему полусумматора удобно синтезировать на основе именно этого элемента и элемента И (рис. 8.25,а).
Полный сумматор на примере одноразрядного устройсвта выполняет операцию арифметического сложения двух одноразрядных чисел A и B с учетом переноса из младшего разряда Р-1. Он имеет три входа и два выхода. Работа полного одноразрядного сумматора задается таблицей истинности 8.11:
Таблица 8.11
| Входы | Выходы | |||
| A | B | Р-1 | S | P |
СДНФ для переменных S и P одноразрядного полного сумматора после ряда тождественных преобразований следующие:
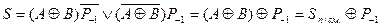 ,
,
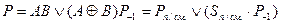 .
.
Выражение 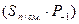 есть ни что иное, как значение выхода переноса полусумматора над величинами Sп/см. и Р-1. Учитывая этот факт и анализируя полученные логические уравнения, можно сделать заключение о возможности реализации полного сумматора на основе двух полусумматоров и одного элемента ИЛИ. Схема полного одноразрядного сумматора представлена на рис. 8.25,б, а УГО одноразрядных полусумматора и сумматора соответственно на рис. 8.25,в и рис.8.25,г.
есть ни что иное, как значение выхода переноса полусумматора над величинами Sп/см. и Р-1. Учитывая этот факт и анализируя полученные логические уравнения, можно сделать заключение о возможности реализации полного сумматора на основе двух полусумматоров и одного элемента ИЛИ. Схема полного одноразрядного сумматора представлена на рис. 8.25,б, а УГО одноразрядных полусумматора и сумматора соответственно на рис. 8.25,в и рис.8.25,г.

Рис.8.25. Схема функциональная одноразрядного полусумматора на элементах «исключающее ИЛИ» и конъюнкторе (а), полного одноразрядного сумматора на базе двух полусумматоров (б), УГО одноразрядных полусумматора (в) и полного сумматора (г).
Схему полного сумматора можно также реализовать и на вентилях элементарных функций в базисе И-ИЛИ-НЕ. Из таблицы истинности 8.11 полного одноразрядного сумматора очевидно, что на выходе суммы S формируется единица, а на выходе переноса Р – ноль при наличии единицы на одном из входах A, B или Р-1. При наличии единиц на любых двух из трех входов полного сумматора, на выходе S будет ноль, а на выходе P – единица. При наличии на всех трех входах логических единиц, на обоих выходах сумматора присутствуют единицы. При нулях на всех трех входах выходы также принимают нулевые состояния. Структура, реализующая описанное правило и положенная в основу микросхем сумматоров 155 и 555 серий, приведена на рис. 8.26.
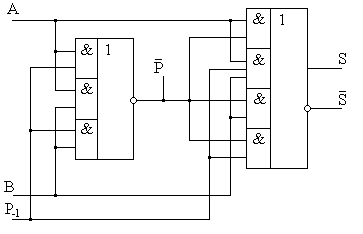
Рис. 8.26. Функциональная схема одноразрядного полного сумматора в базисе И-ИЛИ-НЕ.
При суммировании многоразрядных двоичных чисел с помощью одноразрядных сумматоров их соединяют в последовательные структуры, как это показано на рис.8.27. В этой схеме переносы передаются последовательно путем соединения выходов переносов 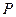 одноразрядных сумматоров младших разрядов с входами переносов
одноразрядных сумматоров младших разрядов с входами переносов 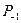 одноразрядных сумматоров старших разрядов. Вход переноса одноразрядного сумматора самого младшего разряда заземляется, что равносильно подаче на него логического нуля. Такой способ наращивания разрядности достаточно прост в схемной реализации, но при этом имеет существенный недостаток – низкое быстродействие. Общее время срабатывание схемы всего сумматора будет равно времени срабатывания одного сумматора, умноженного на количество разрядов. Таким образом, чтобы не считать ошибочный код, считывание информации с устройства возможно только по прошествии указанного времени.
одноразрядных сумматоров старших разрядов. Вход переноса одноразрядного сумматора самого младшего разряда заземляется, что равносильно подаче на него логического нуля. Такой способ наращивания разрядности достаточно прост в схемной реализации, но при этом имеет существенный недостаток – низкое быстродействие. Общее время срабатывание схемы всего сумматора будет равно времени срабатывания одного сумматора, умноженного на количество разрядов. Таким образом, чтобы не считать ошибочный код, считывание информации с устройства возможно только по прошествии указанного времени.
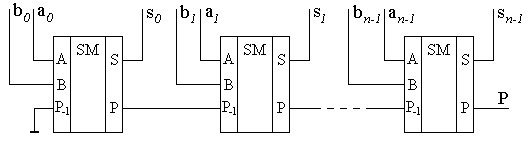
Рис. 8.27. Схема функциональная сумматора с последовательной передачей переноса.
Существет способ организации структуры многоразрядного сумматора, в которой переносы во все разряды формируются одновременно с подачей входных кодов складываемых чисел. Т.е. переносы подаются на все входы одновременно или, иными словами, параллельно. Поэтому такая структура получила название сумматора с параллельным переносом.
Выражение для переноса в старший разряд одноразрядного полного сумматора можно преобразовать к следующему виду
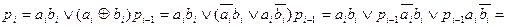

Введем обозначения 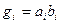 и
и  , где gi – функция переноса, hi – функция передачи переноса. Тогда
, где gi – функция переноса, hi – функция передачи переноса. Тогда
 .
.
В общем случае можно записать
 ,
,
где  - перенос в самый младший разряд из предыдущего сумматора, если таковой предусмотрен в структуре цифрового устройства. В противном случае
- перенос в самый младший разряд из предыдущего сумматора, если таковой предусмотрен в структуре цифрового устройства. В противном случае  =0. Таким образом, сигнал pi можно получить одновременно с появлением всех разрядов аi и вi на входах сумматора, не дожидаясь формирования переноса в отдельных разрядах полных одноразрядных сумматоров. В случае четырехразрядных чисел А и В можно записать
=0. Таким образом, сигнал pi можно получить одновременно с появлением всех разрядов аi и вi на входах сумматора, не дожидаясь формирования переноса в отдельных разрядах полных одноразрядных сумматоров. В случае четырехразрядных чисел А и В можно записать
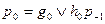 ,
,
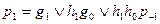 ,
,
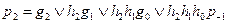 .
.
Для построения четырехразрядного сумматора с параллельным переносом необходимо полученные ФАЛ для pi каждого разряда реализовать в каком-либо базисе, например И-НЕ. Далее выходные сигналы pi с каждой части такой комбинационной схемы должны быть поданы на соответствующие входы Р-1 полных одноразрядных сумматоров. Пример такой структуры приведен на рис. 8.28.
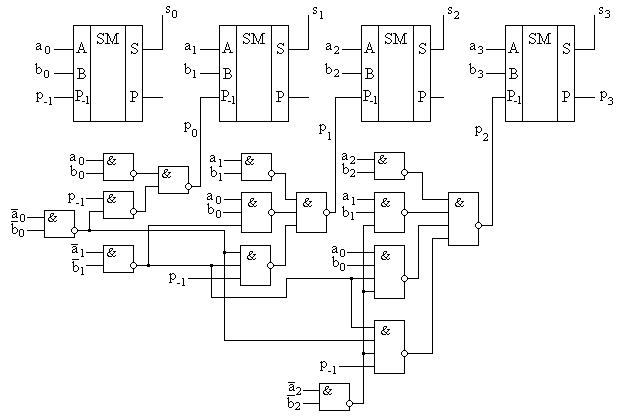
Рис. 8.28. Схема функциональная четырехразрядного сумматора с параллельным переносом.
Из рисунка видно, что даже для четырехразрядного сумматора требуется достаточно сложная комбинационная схема формирования переноса. Поэтому схемы сумматоров с параллельным переносом в интегральном исполнении реализуют обычно для сложения чисел с разрядностью не более четырех бит. При необходимости реализации быстродействующих сумматоров для сложения двоичных чисел большей разрядности используют два подхода. Первый заключается в использовании микросхем полных сумматоров с параллельным переносом в качестве базовых элементов и объединении их в общую последовательную структуру. Сумматоры, реализованные по такой структуре, называются сумматорами с цепным переносом. Подобная структура не может обладать максимальным быстродействием, но при этом является простой в схемотехнической реализации. Второй подход также основан на использовании набора микросхем сумматоров с параллельным переносом. Но их объединение в общую структуру основано на принципе параллельной передачи переноса. В этом случае требуется дополнительная комбинационная схема, реализующая параллельный перенос между параллельными сумматорами. Сумматоры с такой структурой называются параллельно-параллельными. Они имеют максимальное быстродействие, но их реализация требует дополнительных аппаратных затрат.
Сумматор является основой для многих схем выполнения арифметических операций над двоичными и двоично-десятичными кодами. Кроме собственно суммирования, сумматоры используются в перемножителях. Умножение в двоичном коде выполняется аналогично умножению десятичных чисел – столбиком. Приведем в качестве примера выполнение умножения столбиком двух трехразрядных двоичных чисел:
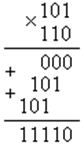
Из примера видно, что умножение реализуется операциями суммирования и сдвига. Существует несколько методов построения умножителей. Наиболее проста в схемотехнической реализации матричная организация перемножителя на базе сумматоров, показанная на рис.8.29. Эта схема иллюстрирует построение умножителяля трехразрядных положительных двоичных чисел. Для формирования произведения трехразрядных двоичных чисел требуется вычислить три частичных произведения. Обратите внимание, что в двоичной арифметике требуется выполнять умножение только на числа 0 и 1. Поскольку в одном разряде правила выполнения арифметического и логического умножений совпадают, то для формирования частичного произведения можно воспользоваться логическими элементами «2И».
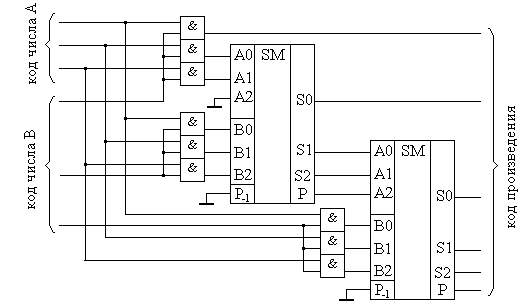
Рис.8.29. Схема матричного перемножителя трехразрядных двоичных положительных чисел.
Для формирования частичного произведения, кроме операции умножения на один разряд, требуется осуществлять его сдвиг влево на число разрядов, соответствующее весу разряда множителя. Сдвиг можно осуществить простым соединением соответствующих разрядов частичных произведений к необходимым разрядам двоичных сумматоров. Первый сумматор суммирует первое и второе частные произведения. При этом самый младший разряд первого частного произведения согласно примеру не нуждается в суммировании. Поэтому он подаётся на выход умножителя непосредственно. А два остальных разряда первого частного произведения подаются на входы A первого сумматора со смещением вправо на один разряд. На свободный старший разряд входов A первого сумматора достаточно подать незначащий ноль (т.е. просто заземлить этот вход). Второе частное произведение подается на входы B первого сумматора без смещения. Точно таким же образом осуществляется суммирование третьего частного произведения. Отличие заключается только в том, что на старший разряд входов A второго сумматора подается сигнал переноса с выхода первого сумматора. Таким образом, сдвиг в схеме матричного перемножителя осуществляется за счет смещения на один разряд частных произведений и подачи их на входы сумматоров следующих разрядов с номерами, на единицу меньшими.
Дата добавления: 2022-02-05; просмотров: 1311;











