Представление синусоидальных токов и напряжений векторами. Комплексные токи и напряжения

Синусоидальный ток и его основные параметры

Синусоидальными токами и напряжениями называются токи и напряжения, которые изменяются во времени по синусоидальному закону.

Мгновенные значения синусоидальных тока и напряжения определяются выражениями:

i(t)= I_m sin(ωt + ψ_i), u(t)= U_m sin(ωt + ψ_u),

где I_m, U_m – амплитудные значения тока и напряжения;

(ωt + ψ) – фаза колебания, аргумент синусоидальной функции, [рад];

ω– угловая частота, которая может быть определена как

ω =2πf = 2π/T, [рад/с];

f– линейная частота, [Гц]; Т– период колебаний, [c];

ψ_i , ψ_u - начальные фазы тока и напряжения, которые отсчитываются от начала координат до ближайшей точки на оси абсцисс перехода синусоидальной функции через ноль от отрицательных к положительным ее значениям. Начальная фаза может быть положительной, отрицательной и равной нулю. При ψ>0 начало синусоиды сдвинуто влево относительно начала координат, при ψ < 0 – вправо, а при ψ = 0 синусоида проходит через начало координат.

На рис. 2.1 построены временные графики мгновенных значений тока и напряжения одинаковой частоты:

i(t)= I_m sin(ωt + ψ_i), u(t)= U_m sin(ωt + ψ_u).

Угол, на который синусоида тока сдвинута относительно синусоиды напряжения, называют углом сдвига фаз φ и его определяют как разность начальных фаз напряжения и тока:

φ = ψ_u – ψ_i.

Если угол φ>0, то ток отстает по фазе от напряжения; если угол φ <0, то ток опережает напряжение по фазе; при значении угла φ=0, ток совпадает по фазе с напряжением.

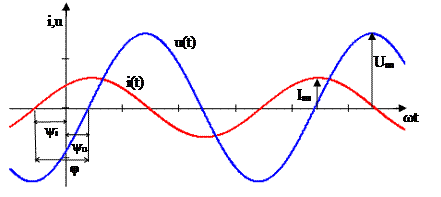Рис. 2.1

Действующие значения синусоидальных ЭДС,

Напряжений и токов

О величине периодических ЭДС, напряжений и токов обычно судят по их средним квадратичным значениям за период, которые называются действующими значениями ЭДС, напряжения или тока и обозначаются, соответственно, E, U, I.

Под действующим значением синусоидального тока i(t)= I_m sin(ωt + ψ_i), понимают такой постоянный ток I, который при протекании через сопротивление R (рис. 2.2) выделяет такое же количество тепла, что и синусоидальный ток за время, равное одному периоду синусоидального тока: .

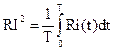Откуда

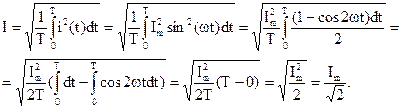Действующие значения ЭДС и напряжения определяются аналогичными соотношениями:

, , .

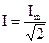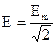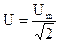Большинство систем измерительных приборов измеряют действующие значения токов и напряжений, поэтому расчеты в цепях синусоидального тока чаще всего выполняют по действующим значениям.

Представление синусоидальных токов и напряжений векторами. Комплексные токи и напряжения

Синусоидальные ЭДС, напряжения и токи, имеющие частоту ω, можно изображать векторами, вращающимися с угловой скоростью, равной ω, причем длина вектора определяется в соответствующем масштабе амплитудой ЭДС, напряжения или тока.

Пусть мы имеем две синусоидальные ЭДС

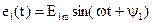и .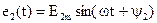

Изобразим их в виде векторов в момент времени равный нулю (рис. 2.3). Начальные фазы этих синусоидальных ЭДС откладываются от горизонтальной оси против часовой стрелки, если они положительны, и по часовой стрелке, если они отрицательны. Длины векторов равны соответствующим амплитудным значениям.

Найдем ЭДС е(t), равную сумме ЭДС е₁(t) и е₂(t). Тогда эта ЭДС е(t) будет изображаться вращающимся вектором, равным геометрической сумме векторов, изображающих ЭДС е₁(t) и е₂(t).

В любой момент времени взаимное расположение этих вращающихся векторов будет оставаться неизменным, поэтому достаточно построить вектора в момент времени равный нулю, и все операции выполнять над ними.

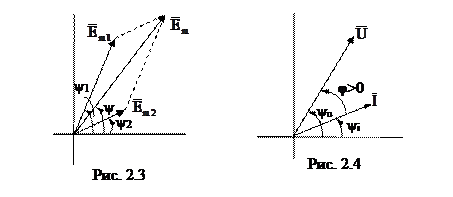Совокупность векторов, характеризующих процессы, происходящие в той или иной цепи синусоидального тока, и построенных с соблюдением правильной ориентации их друг относительно друга для момента времени равного нулю, называют векторной диаграммой.

Часто при расчетах используются действующие значения синусоидальных функций, которые в 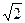раз меньше их амплитуд, в этих случаях целесообразно на векторной диаграмме длину векторов выбирать равной, в избранном масштабе, действующим значениям ЭДС, напряжений или токов. На рис. 2.4 изображена векторная диаграмма напряжения и тока, причем ток отстает от напряжения на угол φ, который на векторной диаграмме всегда показывается стрелкой, направленной от вектора тока к вектору напряжения.

Синусоидальную функцию 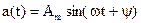можно изобразить вектором (рис. 2.5) на комплексной плоскости или записать в виде комплексного числа в показательной форме

,

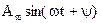
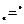
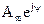где 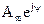- называется комплексной амплитудой.

Комплексная амплитуда представляет собой вектор на комплексной плоскости, длина которого соответствует амплитудному значению синусоидальной функции А_m , а угол ψ – начальной фазе.

При изучении курса ТОЭ пользуются следующими тремя формами записи комплексной амплитуды в виде комплексного числа:

показательная ;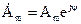

тригонометрическая ;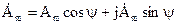

алгебраическая 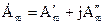, где

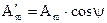- действительная часть комплексного числа;

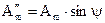- мнимая часть комплексного числа,

Для обратного перехода от алгебраической к показательной форме записи необходимо найти модуль этого комплексного числа с помощью теоремы Пифагора (рис. 2.5) и аргумент путем определения тангенса соответствующего угла:

, .

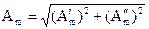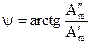Алгебраическая форма удобна при сложении и вычитании комплексных величин, а показательная при умножении, делении, возведении в степень и извлечении корня.

Мнимая единица 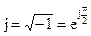называется оператором поворота на угол 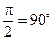. Умножение на 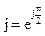сводится к повороту вектора против часовой стрелки на прямой угол, а умножение на 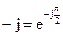- к повороту вектора на прямой угол по часовой стрелке.

Числа 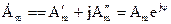и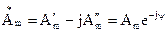

называют комплексно-сопряженными числами. Произведение комплексно-сопряженных чисел - действительное число, равное квадрату их модуля .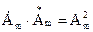

Комплексное действующее значение .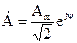

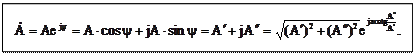Все формы записи комплексной величины и связь между ними записываются