Комплексный метод расчета

Для расчета цепей синусоидального тока используется комплексный метод расчета. Он основан на изображении синусоидальных функций времени комплексными числами. Соответственно дифференциальные и интегральные зависимости между напряжениями и токами в цепях синусоидального тока, заменяются линейными зависимостями между комплексными токами и напряжениями:

→

→

→

→

→

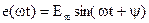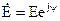
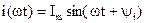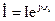
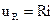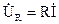
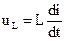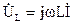
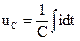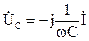
Далее расчеты в цепях синусоидального тока выполняются теми же методами, что и расчеты в цепях постоянного тока (метод эквивалентных преобразований, законов Кирхгофа, контурных токов, узловых потенциалов и т.д.), только все сопротивления, токи и напряжения записываются в комплексной форме записи.

Рассмотрим определение всех токов и напряжений в схеме, показанной на рис.2.19, питающейся от источника синусоидального напряжения, комплексное действующее значение которого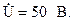

Параметры элементов цепи:

R₁=50 Ом; R₂=X_L=X_C =100 Ом.

Расчет будем выполнять, применяя эквивалентные преобразования в электрических цепях и закон Ома.

Определим комплексные сопротивления ветвей:

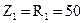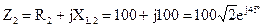Ом; 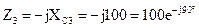Ом;

Ом.

Для того чтобы по закону Ома определить ток на входе цепи, необходимо рассчитать комплексное сопротивление цепи относительно входных зажимов.

Сопротивления второй и третьей ветвей соединены параллельно, поэтому их эквивалентное сопротивление относительно зажимов 2-4 можно рассчитать:

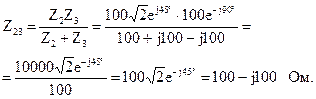
Относительно входных зажимов сопротивление первой ветви и сопротивление Z₂₃ соединены последовательно, поэтому входное сопротивление всей цепи можно определить как сумму комплексных сопротивлений:

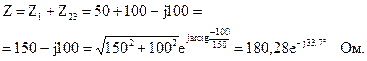
Входной ток

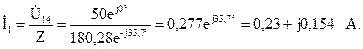
Напряжение на зажимах параллельных ветвей:

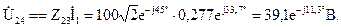
Зная напряжения параллельных ветвей, можно определить по закону Ома токи

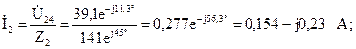
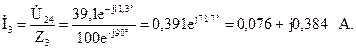
Определим напряжения на участках цепи:

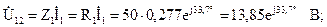
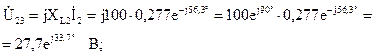
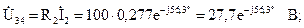
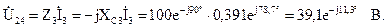
Построим векторную диаграмму токов и напряжений цепи. Для этого на комплексной плоскости в соответствующих масштабах тока m_i и напряжения m_u построим векторы рассчитанных напряжений и токов со своими начальными фазами (рис. 2.20). На векторной диаграмме хорошо видно выполнение законов Кирхгофа:

,

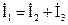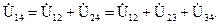
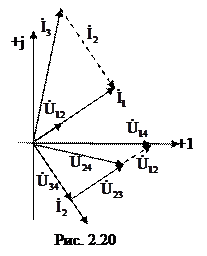2.10. Топографическая диаграмма

При анализе электрических цепей синусоидального тока весьма полезно строить топографические диаграммы. С их помощью можно легко определять напряжения между различными точками схемы и фазы этих напряжений. Топографическая диаграмма представляет собой графическое изображение на комплексной плоскости распределения потенциалов в схеме. При этом каждой точке схемы соответствует определенная точка на топографической диаграмме.

Отличительная особенность этих диаграмм состоит в том, что векторы напряжений на зажимах элементов сложной цепи на топографической диаграмме располагают в том порядке, в котором расположены соответствующие элементы цепи. При этом вектор напряжения на последующем элементе цепи обязательно примыкает к вектору напряжения на предыдущем элементе, в то время как на обычных векторных диаграммах любой вектор можно переносить параллельно самому себе в любое место комплексной плоскости.

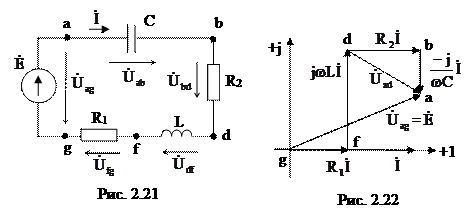
Проведем качественное построение топографической диаграммы для неразветвленной цепи (рис. 2.21).

Отложим вектор тока 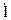в произвольно выбранном направлении (рис. 2.22). Примем потенциал точки g равным нулю ( 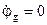) и определим потенциалы остальных точек схемы относительно этого потенциала. Обход схемы при построении топографической диаграммы выберем навстречу току. Тогда потенциал точки f будет больше потенциала точки g на величину напряжения на резисторе R₁: 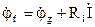. Наносим вектор 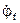на комплексную плоскость и конец этого вектора обозначаем буквой f. Причем сам вектор комплексного потенциала не изображается на плоскости, а показывается только

точка, соответствующая концу этого вектора.

Аналогично рассчитываем и наносим на комплексную плоскость потенциалы остальных точек схемы:

; ; .

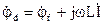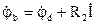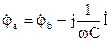Для определения напряжения между двумя любыми точками схемы достаточно соединить соответствующие точки топографической диаграммы отрезком прямой и придать этому вектору надлежащее направление. Так, вектор напряжения 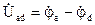представлен на топографической диаграмме отрезком прямой, соединяющим точки а и d, соответствующие концам векторов комплексных потенциалов 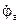и 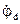. Этот вектор направлен от точки d к точке а, что соответствует правилу вычитания векторов.

Топографическую диаграмму практически всегда строят в одних осях координат с векторной диаграммой токов.

Заметим, что при выборе обхода ветвей схемы навстречу положительному направлению тока топографическая диаграмма совпадает с понятием векторной диаграммы. То есть ее можно строить, употребляя привычные нам знания: напряжение на резисторе совпадает по фазе с током, напряжение на индуктивном элементе опережает ток на угол 90º, а на емкостном элементе напряжение отстает от тока на угол 90º.

При выборе обхода схемы по току все векторы изменяют свое направление на 180º.