Частотные характеристики и передаточные функции

К частотным характеристикам цепи относятся входные и передаточные функции. К комплексным частотным характеристикам относятся входные и передаточные функции, записанные в комплексной форме. Входная комплексная функция цепи – это зависимость от частоты входного комплексного сопротивления или проводимости относительно двух выделенных или заданных зажимов:

,

.

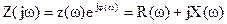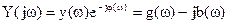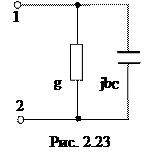В качестве примера построим зависимости от частоты модуля сопротивления z(ω) и аргумента φ(ω) входного комплексного сопротивления схемы замещения реального конденсатора (рис. 2.23) с заданными параметрами 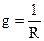и С. Будем считать их в рассматриваемом диапазоне частот постоянными.

Входное сопротивление:

,

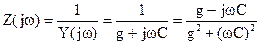тогда выражения для построения характеристик можно записать:

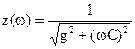и .

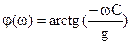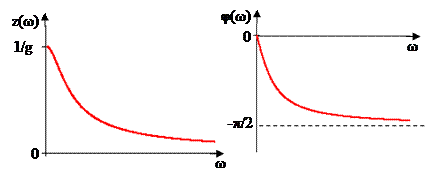
Эти зависимости показаны на рис. 2.24.

Рис. 2.24

Передаточная комплексная функция (коэффициент передачи) цепи определяет реакцию цепи на внешнее воздействие и равно отношению выходной величины напряжения или тока к входной величине напряжения или тока, выраженных в комплексной форме.

Различают четыре вида передаточных функций:

- передаточная функция по напряжению: ;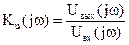

- передаточная функция по току: ;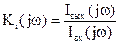

- передаточное сопротивление: ;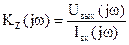

- передаточная проводимость: .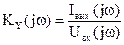

Передаточные функции 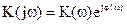могут определяться для различных пар выбранных входных и выходных выводов цепи.

Зависимость модуля передаточной функции К(ω) от частоты называется амплитудочастотной характеристикой (АЧХ), зависимость аргумента передаточной функции φ(ω) - фазочастотной характеристикой (ФЧХ).

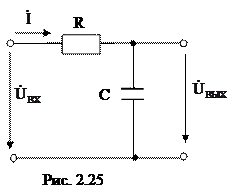В качестве примера рассмотрим передаточную функцию по напряжению цепи, схема которой приведена на рис. 2.25.

Передаточная функция определяется как отношения выходного напряжения цепи в режиме холостого хода к входному напряжению:

.

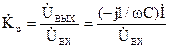Ток цепи определим по закону Ома: ,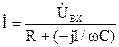

отсюда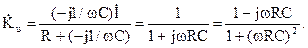

Амплитудочастотная характеристика (АЧХ) имеет вид:

;

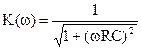а фазочастотная (ФЧХ):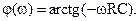

Графики этих зависимостей аналогичны графикам, приведенным на рис. 2.24.