Методика замены нескольких действительных неосновных полюсов в передаточной функции операционного усилителя одним «эффективным» неосновным полюсом
Пусть в операционном усилителе кроме основного полюса 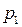 имеются два неосновных,
имеются два неосновных, 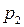 и
и 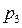 . Передаточная функция в этом случае:
. Передаточная функция в этом случае:
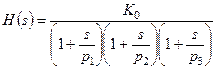 (4.9)
(4.9)
Рассмотрим произведение 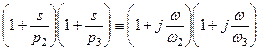 .
.
Преобразуем его:
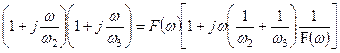 , где
, где 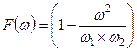 (4.10)
(4.10)
Очевидно, что знак дискриминанта в (4.5) необходимо рассматривать на частотах, близких к 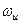 , пока коэффициент усиления хотя бы на ничтожную величину больше единицы. Пусть
, пока коэффициент усиления хотя бы на ничтожную величину больше единицы. Пусть 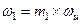 и
и 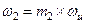 . В этом случае при
. В этом случае при 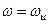 имеем
имеем
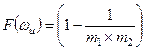 (4.11)
(4.11)
Поскольку коэффициенты 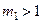 и
и 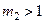 , т.е. всегда больше единицы в несколько раз, то произведение этих коэффициентов уже много больше единицы и
, т.е. всегда больше единицы в несколько раз, то произведение этих коэффициентов уже много больше единицы и 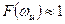 . Отсюда следует, что на критичной частоте
. Отсюда следует, что на критичной частоте 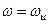 в передаточной функции (4.9) произведение
в передаточной функции (4.9) произведение 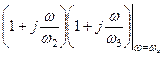 можно формально заменить на
можно формально заменить на
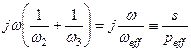 (4.12)
(4.12)
где 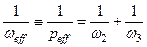 (4.13)
(4.13)
Методику легко распространить на большее количество полюсов. Действительно, подставляя (4.13) в (4.9), получаем передаточную функцию 2-го порядка: 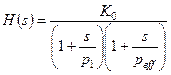 (4.14)
(4.14)
При добавлении третьего неосновного полюса, возвращаемся к (4.9).
Предлагаем без доказательства выражение для эффективной частоты 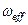 эффективного действительного полюса
эффективного действительного полюса 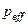 в ОУ с многими действительными полюсами и нулями. Нули могут быть как в отрицательной, так и в положительной полуплоскостях. Выражение справедливо для частот, близких к частоте единичного усиления.
в ОУ с многими действительными полюсами и нулями. Нули могут быть как в отрицательной, так и в положительной полуплоскостях. Выражение справедливо для частот, близких к частоте единичного усиления.
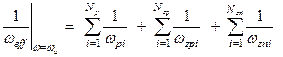 (4.15)
(4.15)
Здесь: 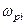 – собственная круговая частота i-го неосновного полюса;
– собственная круговая частота i-го неосновного полюса;
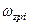 – собственная круговая частота i-го нуля в положительной
– собственная круговая частота i-го нуля в положительной
полуплоскости;
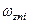 – собственная круговая частота i-го нуля в отрицательной
– собственная круговая частота i-го нуля в отрицательной
полуплоскости.
Противоположное влияние на 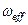 нулей в положительной и отрицательной полуплоскостях отражает тот факт, что при наличии нулей в отрицательной полуплоскости система является минимальнофазовой –и наоборот, при нулях в положительной полуплоскости система – неминимальнофазовая.
нулей в положительной и отрицательной полуплоскостях отражает тот факт, что при наличии нулей в отрицательной полуплоскости система является минимальнофазовой –и наоборот, при нулях в положительной полуплоскости система – неминимальнофазовая.
Дата добавления: 2022-02-05; просмотров: 520;











