Введение в реализацию ARC биквада

Известно [2 – 4],чтопередаточная функция(ПФ) фильтра в общем случае выражается отношением полиномов:

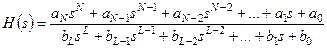(1.27)

где, как правило, 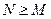. При действительных коэффициентах корни полиномов могут быть либо действительными, либо комплексно–сопряженными, поэтому одним из способов реализации фильтра является разложение на произведение 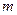простых дробей, в которых числители и знаменатели являются полиномами не выше второго порядка:

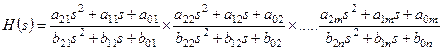(1.28)

Из свойств преобразования Лапласа вытекает, что если ПФ всей системы равна произведению всех ПФ всех подсистем, то эти подсистемы включены последовательно друг за другом. Таким образом, произвольный линейный фильтр высокого порядка, описываемый рациональной дробью, реализуется последовательным включением фильтров порядка не более двух! Подобная многокаскадная архитектура активного фильтра высокого порядка является наиболее простой.

Фильтр, описываемый рациональной дробью второго порядка, называется биквадом.

Пусть передаточная функция биквада имеет вид:

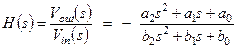(1.29)

Знак «минус» перед дробью не играет принципиальной роли, но с ним реализация ARC фильтра получается проще.

В дальнейшем в записи ПФ биквада будем следовать традиции, сформировавшейся при решении в электротехнических задачах с помощью дифференциальных уравнений второго порядка, а, именно, записывать ПФ биквада в канонической форме (см. выражение (1.15)):

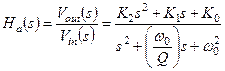(1.30)

Здесь 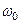- частота полюса, а 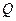-добротность полюса.

Пусть для краткости записи выражений 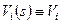. Перепишем в этом случае выражение (1.25) в виде:

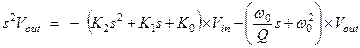(1.31)

Делим обе части на 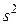и проводим перекомпоновку:

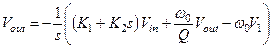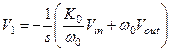, где (1.32)

Функциональная схема биквада, описываемая уравнением (1.30), приведена на рис. 1.6.

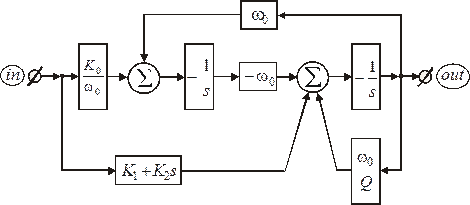
Рис. 1.6. Функциональная схема биквада.

Определим электротехническую реализацию алгебраических многочленов в выражении (1.30) и на рис. 1.6. Для этого отметим, что при записи уравнений Кирхгофа узел А инвертирующего входа ОУ в активном интеграторе вместе с интегрирующим конденсатором С выполняет роль коллектора токов компонентов, подключенных к этому узлу.

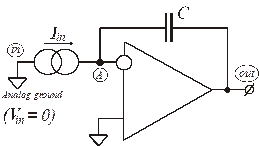Найдем ПФ интегратора тока, представленного на рис. 1.7, с входной переменной, являющейся током 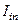и выходной переменной, являющейся напряжением .

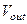Рис. 1.7. Активный

инвертирующий интегратор

с токовым входом.

Итак:

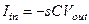; В этом случае 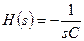. (1.33а)

Если 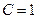, то 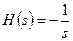, что и требовалось. (1.33b)

Следует далее помнить, что несмотря на то, что формально (точнее – по внешнему виду) передаточная функция активного инвертирующего интегратора с токовым входом определяется выражением (1.33b), во всех попытках синтеза биквада следует помнить, что в выражении (1.33b) в скрытом виде находится параметр, соответствующий интегрирующей емкости с номиналом в 1Ф.

Найдем теперь ПФ параллельной RC цепочки, но, наоборот, с напряжением на входе и с током на выходе. Такая цепочка изображена на рис. 1.8.

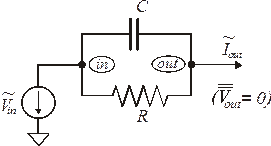
Рис. 1.8. Параллельная

RC цепочка с напряжением

на входе и током на выходе.

Поставим дополнительное условие, а, именно, потенциал токового выхода поддерживается равным нулю, предполагая, что этот токовый выход должен быть подключен к инвертирующему входу идеального интегратора с токовым входом, изображенному на рис. 1.7. Итак, имеем:

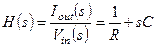отсюда, если 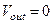, то 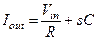. (1.34)

Сравниваем со схемой на рис. 1.6 и находим блок, содержащий многочлен, содержащий переменную 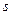. Поскольку коэффициент при переменной 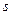обязательно должен содержать емкость 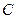, то делаем вывод, что коэффициент 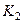есть значение емкости, а свободный член 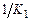есть обратное значение сопротивления, т.е. значение проводимости. Аналогично 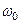и 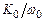– также значения проводимостей, а 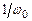и 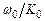– значения сопротивлений. Согласно нашим рассуждениям, член 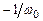является также значением сопротивления, но отрицательным. Этот факт не должен вызывать затруднений, поскольку это просто означает, что перед резистором с положительнойвеличиной 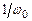должен находиться инвертор сигнала, подобный изображенному на рис.1.4.

Существует, однако, более приемлемое техническое решение, реализация которого воплощает уже практически повсеместно сложившуюся тенденцию использования полностью дифференциальных операционных усилителей (усилители как с дифференциальными входами, так и дифференциальными выхода микросхем. Последнее подразумевает наличие двух выходов с противофазными выходными сигналами). Количество компонентов в фильтрах на базе полностью дифференциальных операционных усилителей, очевидно, удваивается по сравнению с функционально аналогичными схемами, но на базе усилителей с единственным выходом. Описание характеристик подобных ОУ и схем на их основе излагается в главе V, здесь же изложение материала предполагает интуитивное понимание существа вопроса.

С учетом (1.31) и (1.32), АRC реализация биквада с использованием полностью дифференциальных ОУ приведена на рис. 1.9.

Как видно из рис. 1.9, инвертирование сигнала с выхода первого ОУ потребовало НЕ дополнительного ОУ, а всего лишь взаимную замену полярностей выходов первого ОУ на входы второго интегратора.

Обращаем внимание на принципиальный тезис: В активных фильтрах основой элементной базы являются активные интеграторы.