Принцип масштабирования пассивных элементов в ARC фильтрах
Разумеется, ни в интегральных ARC фильтрах, ни в фильтрах на дискретных компонентах, не используют номинал 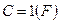 для конденсатора, и чрезвычайно редко – номинал
для конденсатора, и чрезвычайно редко – номинал 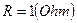 для резистора.
для резистора.
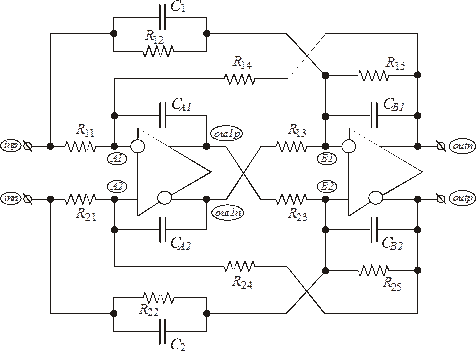
Рис. 1.9. Электрическая схема АRC биквада с использованием полностью дифференциальных операционных усилителей.
Реализация активных фильтров на интегральной схеме возможна благодаря существованию метода так называемого масштабирования.
Запишем, например, для узла 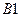 уравнение Кирхгофа:
уравнение Кирхгофа:
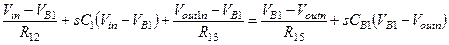 (1.35)
(1.35)
Разделим обе части уравнения (1.33) на 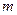 и сгруппируем коэффициенты соответствующим образом:
и сгруппируем коэффициенты соответствующим образом:
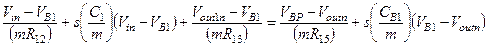 (1.36)
(1.36)
Итак, уравнение (1.34) выражает правило:
Для установления реальных значений номиналов резисторов и конденсаторов во всех ветвях, подходящих к узлу виртуальной аналоговой земли операционного усилителя, номиналы резисторов можно увеличить в какое-либо количество раз, а номиналы конденсаторов – уменьшить в такое же количество раз. Пределы этого масштабирования,как правило,ограничиваются размерами интегральных резисторов и паразитными емкостями.
Тем не менее, само по себе масштабирование не позволяет перешагнуть через физические ограничения на номиналы компонентов, а, именно, интегральные конденсаторы трудно сделать с емкостью, большей, чем 50 пФ, а резисторы – с сопротивлением, большим 1Мом. Тем не менее, даже такие компоненты имеют весьма значительные площади, поэтому с их помощью весьма трудно создавать фильтры относительно низких, например, звуковых, частот. В дополнение следует отметить, что конденсаторы и резисторы формируются разными технологическими операциями, поэтому имеют взаимно независимые разбросы номиналов, что приводит к большому разбросу постоянных времени, т.е. произведений номиналов и, соответственно, значительному разбросу частот среза амплитудно-частотных характеристик. Использование концепции переключаемых конденсаторов позволяет, во-первых, создавать низкочастотные фильтры и, во-вторых, обеспечивать высокую точность частот среза амплитудно-частотных характеристик.
Дата добавления: 2022-02-05; просмотров: 420;











