Инвертирующий усилитель

Аналогично предыдущему примеру, составляем систему линейных уравнений для схемы инвертирующего усилителя на рис. 1.4. Пусть для краткости записи выражений :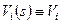

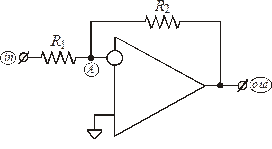
Рис. 1.4. Инвертирующий

усилитель

Уравнения Кирхгофа:

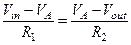(1.20а)

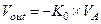(1.20b)

Выражение для передаточной функции имеет вид:

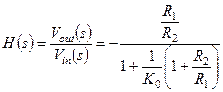(1.21)

При условии 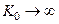имеем знакомый из учебников вид передаточной функции:

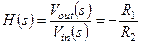(1.22)

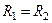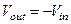Если , то , т.е. схема инвертирует знак входной переменной и является инвертором сигнала.

Активный инвертирующий интегратор

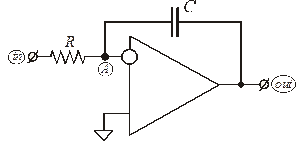
Рис. 1.5. Активный

инвертирующий

интегратор.

Аналогично предыдущему примеру и, cогласно схеме активного инвертирующего интегратора на рис. 1.5, составляем систему линейных уравнений Кирхгофа (операционный усилитель имеет ограниченный коэффициент усиления ):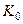

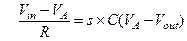(1.23а)

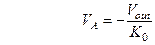(1.23b)

Решая систему (1.21), получаем передаточную функцию:

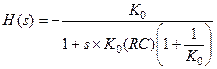(1.24)

При условии 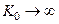выстраивается следующая последовательность упрощений:

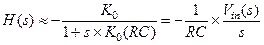(1.25)

Оригинал (во временнòй области) последнего выражения имеет вид:

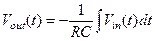(1.26)