Пассивный RC фильтр низких частот первого порядка
Проведем анализ этой простейшей частотозависимой линейной схемы, представленной на рис. 1.1. Эту схему называют интегрирующей RC цепочкой, что следует из уравнения Кирхгофа для оригинала схемы (во временнòй области):
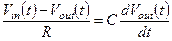 , (1.5)
, (1.5)
откуда после интегрирования 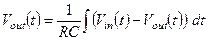 (1.6)
(1.6)
Определим характеристики схемы в частотной области, пользуясь методом преобразования Лапласа.
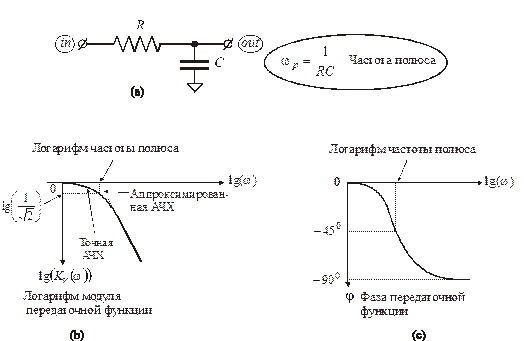
Рис. 1.1: (а) пассивный RC фильтр низких частот первого порядка: (b) зависимость коэффициента передачи от частоты; (с) зависимость сдвига фазы между входным и выходным сигналами от частоты.
Напомним известную из курса теоретической электротехники передаточную функцию пассивного RC фильтра в стационарном состоянии. Для ее получения используем законы Кирхгофа, справедливые как для оригиналов, так и для изображений токов:
Очевидно, что 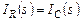 , т.е.
, т.е. 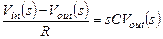 (1.7)
(1.7)
Передаточная функция:
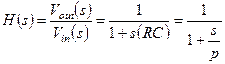 (1.8)
(1.8)
Здесь 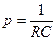 – действительный полюс передаточной функции.
– действительный полюс передаточной функции.
Для стационарного состояния 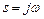 , поэтому
, поэтому
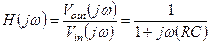 (1.9)
(1.9)
Модуль 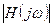 комплексного выражения (1.7) определяет зависимость от частоты коэффициента передачи
комплексного выражения (1.7) определяет зависимость от частоты коэффициента передачи 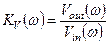 напряжения с входа
напряжения с входа  на выход
на выход 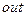 рассматриваемого фильтра:
рассматриваемого фильтра:
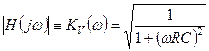 (1.10)
(1.10)
Сдвиг фазы 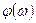 между напряжениями
между напряжениями 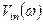 и
и  определяется выражением:
определяется выражением:
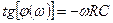 (1.11)
(1.11)
На малых частотах, при которых круговая частота сигнала много меньше собственной круговой частоты полюса передаточной функции, т.е. 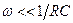 , выражение для
, выражение для 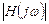 значительно упрощается и аппроксимируется выражением:
значительно упрощается и аппроксимируется выражением:
 (1.12)
(1.12)
На высоких частотах, при которых круговая частота сигнала много больше собственной круговой частоты полюса передаточной функции, т.е. 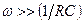 , выражение для
, выражение для 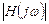 также упрощается, и соответствующая аппроксимация имеет вид:
также упрощается, и соответствующая аппроксимация имеет вид:
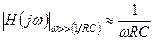 (1.13)
(1.13)
Иллюстрации точных и аппроксимированных зависимостей от частоты коэффициента передачи 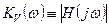 и разности фаз
и разности фаз 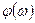 между входным и выходным сигналами представлены на рис. 1.1(b) и 1.1(с) соответственно.
между входным и выходным сигналами представлены на рис. 1.1(b) и 1.1(с) соответственно.
Дата добавления: 2022-02-05; просмотров: 479;











