Одноразрядный двоичный сумматор
Одноразрядный двоичный сумматор является комбинационной схемой с тремя входами и двумя выходами (рис.4.3).
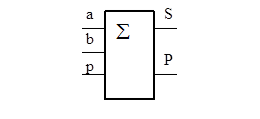
Рис.4.3. Одноразрядный сумматор
Рассмотрим синтез одноразрядного двоичного сумматора
Построение таблицы истинности для одноразрядного сумматора.
При параллельном суммировании на входы каждого разряда сумматора поступают значения цифр а и b соответствующих разрядов слагаемых и значение переноса p с младших разрядов сумматора. На выходе одноразрядного сумматора формируются значения цифры соответствующего разряда суммы Sи переноса в старший разряд сумматора P.
Значения S и P таблицы истинности одноразрядного сумматора (табл. 5) построена на основе таблицы сложения и умножения для двоичной системы счисления (табл.2, раздел 1.3.4).
Таблица 5. Таблица истинности одноразрядного сумматора
| № | Входы | Выходы | |||
| a | b | p | S | P | |
Формирование логических функций выходов
Для каждого выходного сигнала составляются все комбинации входных сигналов (сборка совпадений), при которых выходные сигналы S и P принимают единичные значения:
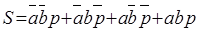 ,
,
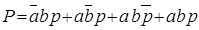 .
.
Эти уравнения являются совершенной дизъюнктивной нормальной формой логических функций (СДНФ). В этой форме логическая функция (ЛФ) представляется в виде дизъюнкций минтермов.
Минтерм – это конъюнкция всех значений входных переменных в прямой форме для единичных значений переменных, или в инверсной форме для нулевых значений переменных.
СДНФ позволяет записывать любые переключательные функции от двух переменных, используя только три основные логические операции И, ИЛИ, НЕ.
Следующим этапом проектирования является минимизация логических функций (не всегда возможна).
Минимизация логических функций.
Преобразование производится на основе свойств логических операций (см. раздел 4.1.
Минимизацию можно производить непосредственно по таблице истинность или по ее специальным формам, таким, как таблица Карно, используя обычную логику и рассматривая выходные переменные как высказывания.
Из таблицы истинности (табл. 5.) видно, что переменная P принимает значение единицы только для таких комбинаций входных переменных, когда хотя бы две переменные имеют единичные значения. Это можно записать в виде:
P = ab + ap + bp.
Для проверки правомерности указанного подхода получим этот же результат на основе преобразования ЛФ для выхода Р.
На основе свойства идемпотентности (A+A = A) в ЛФ для выхода Р минтерм abp можно повторить три раза:
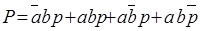 =
= 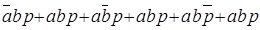 .
.
Группируя минтермы и вынося парные переменные за скобки, получаем:
Р = 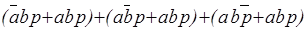 =
=
= 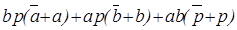 .
.
На основе свойств исключения третьего (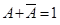 )и конъюнкции
)и конъюнкции
(A1 =A) получаем искомый результат: P = bp1 + ap1 +ab1 = ab + ap + bp.
Минимизация ЛФ выхода S.
Анализируя функцию S, можно заметить, что значение S значение равно единице, если в комбинациях входных сигналов присутствует хотя бы один единичный сигнал (компонента: a+b+p) и нет одновременно двух единичных значений переменных (компонента: 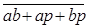 =
= 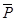 ), или есть совпадение трех входных единичных сигналов (компонента abp), т.е.:
), или есть совпадение трех входных единичных сигналов (компонента abp), т.е.:
Анализируя функцию S, можно заметить, что ее значение равно единице, если в комбинациях входных сигналов ровно один сигнал равен единице или все входные сигналы одновременно равны единице.
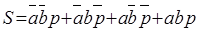
a+b+p
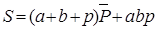
Построение функциональной схемы по ЛФ:
P = ab + ap + bp
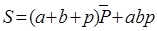
Для реализации ЛФ для выхода Р требуется :
· три конъюнктора (схемы И) на два входа,
· дизъюнктор (схема ИЛИ) на 3 входа.
Для реализации ЛФ для выхода S требуются:
· дизъюнктор (схема ИЛИ) на 3 входа,
· инвертор (схема НЕ),
· конъюнкторы (схемы И) на 2 и 3 входа.
· дизъюнктор (схема ИЛИ) на 2 входа.
Функциональная схема одноразрядного сумматора представлена на рис.4.4.
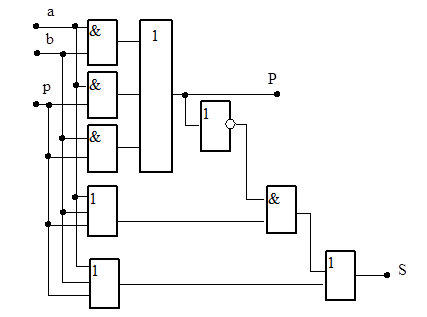
Рис.4.4. Схема одноразрядного сумматора
В этой схеме использована совместная минимизация уравнений, при которой для формирования разных выходных значений (S и P) используются общие логические схемы. Совместная минимизация позволяет получать схемы с минимальным количеством используемых элементарных вентилей, которое определяется по общему количеству входов. Такие схемы, как правило, имеют большую задержку выходных сигналов, которая определяется по максимальному количеству элементов пути его формирования.
По этой причине часто одноразрядный сумматор строят без совместной минимизации схем формирования выходных сигналов по уравнениям:
P = ab + ap + bp,
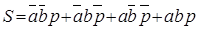 .
.
Обычно в ЭВМ используют обработку данных параллельно по разрядам. Для такой обработки используются параллельные сумматоры.
Сумматор для параллельной обработки данных получают на основе поразрядного соединения одноразрядных схем.
Пример построения многоразрядного сумматора представлен на рис. 4.5.
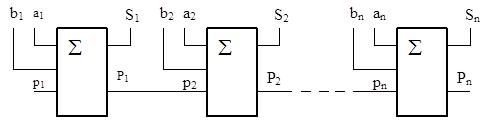
Рис.4.5. Схема параллельного сумматора
Сумматор имеет 2n входных разрядных линий ai и bi для приема цифр слагаемых, n выходных линий Sn разрядов суммы, выход переноса Рn из старшего разряда и вход переноса р0 на младший разряд сумматора.
На функциональных схемах многоразрядные функциональные узлы обозначаются в виде прямоугольников с тремя полями (рис.4.6).
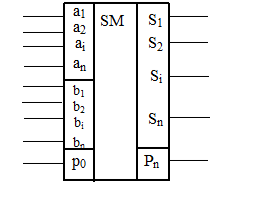
Рис. 4.6. Параллельный сумматор
В основном поле обозначается функциональное назначение схемы. Для сумматора это SM,СМ,å.
Боковые поля предназначены для обозначения данных: правое поле для входных данных, левое – для выходных. Боковые поля могут иметь секции для разделения разноименных входных или выходных данных.
Дешифраторы
Дешифратор – это устройство, которое имеет N входов и 2N выходов, причем каждой i-той комбинации сигналов на входе соответствует сигнал на одном определенном 2i-том выходе. Другими словами, дешифратор – это устройство, которое дешифрирует число в позицию. В частных случаях, дешифратор может содержать меньшее (< 2N) количество выходов. Это неполные дешифраторы. Дешифраторы предназначены для декодирования (распознавания) кодовых комбинаций (адрес устройства, код операции и т. д.).
Рассмотрим синтез дешифратора на 3 входа и на 8 входов. Таблица истинности дешифратора на три входа представлена в табл. 6.
Таблица 6. Таблица истинности дешифратора на три входа
| Входы | Номер активной выходной шины Di и ЛФ выхода. | ||
| a | b | с | |
0 – D0 = 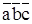
| |||
1 – D1 = 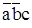
| |||
2 – D2 = 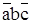
| |||
3 – D3 = 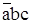
| |||
4 – D4 = 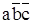
| |||
5 – D5 = 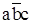
| |||
6 – D6 = 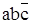
| |||
7 – D7 = 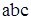
|
Дешифратор на три входа содержит восемь конъюнкторов, каждый на три входа, и три инвертора.
Схема дешифратора на три входа и его обозначение на функциональных схемах представлены на рис. 4.7. Для обозначения функционального назначения схемы для дешифраторов используются символы DC, ДШ. Представленный на рис. 4.7 дешифратор имеет дополнительный вход синхросигналов. Использование синхросигналов позволяет задерживать выходные сигналы на выходе дешифратора на время переходных процессов после смены входных переменных.
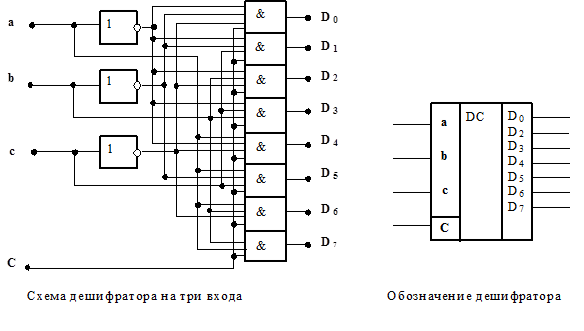
Рис. 4.7. Схема дешифратора и его обозначение на функциональных схемах.
Мультиплексор
Мультиплексор (рис. 4.8.) –это электронное устройство, которое имеет несколько информационных D-входов и один выход Q.
Мультиплексор осуществляет последовательное подключение входов к выходу в соответствии с адресным кодом, поступающим на дополнительные адресные входы (S1, S2).
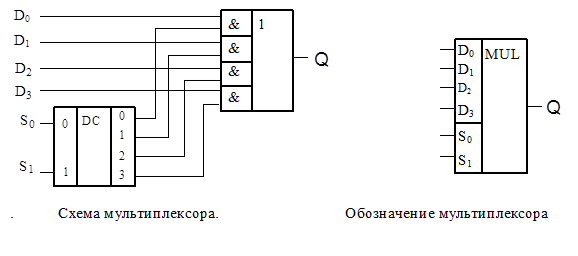
Рис. 4.8. Схема мультиплексора и его обозначение
на функциональных схемах
Функционирование мультиплексора описывается таблицей состояний (табл. 7).
Таблица 7. Таблица состояний мультиплексора
| № | S1 | S2 | QS |
| D0 | |||
| D1 | |||
| D2 | |||
| D3 |
Мультиплексор содержит дешифратор адресного кода, двухвходовые схемы И (по числу выходов мультиплексора) и многовходовую (по числу выходов мультиплексора) схему ИЛИ.
Возможно использование дополнительного элемента И на выходе схемы для стробирования по времени выходного сигнала.
Демультиплексор
Демультиплексор – это устройство, имеющее один информационный вход D и несколько выходов Q, осуществляющее передачу сигнала с информационного входа на один из выходов в соответствиис адресным кодом, поступающим на дополнительные адресные входы (S1, S2). В простейшем случае, в качестве демультиплексора может использоваться дешифратор, у котороговместо сигнала OE подается информационный сигнал X. Например, если на входы подать код a1a0=10(BIN)=2(DEC), a1a0=10(2)=2(10),, то сигнал X появится на выходе y2, а на остальных выходах yi=0. единичный сигнал появится на выходе y2, а на остальных выходах будут нули. На рис. 4.9 представлено обозначение демультиплексора на функциональных схемах.
Рис. 4.9. Обозначение демультиплексора на функциональных схемах
Дата добавления: 2022-02-05; просмотров: 1042;











