Основы математической логики

Электронные цифровые устройства базируются на элементах, входные и выходные сигналы которых могут принимать только одно из двух значений : ноль или единица. Это переключательные элементы. Некоторые из элементов могут иметь третье состояние, но это состояние является состоянием элемента, отключенного по выходу от других элементов (состояние высокого импеданса по выходу).

В зависимости от физической реализации элемента в качестве единичного сигнала (логической 1) может использоваться более положительное значение физической величины тока или напряжения (положительная логика) или менее положительное значение (отрицательная логика).

Логической основой проектирования цифровых устройств на переключательных элементах является алгебра логики или булева алгебра.

Эта алгебра разрабатывалась в рамках "чистой" математики как алгебра высказываний для вычисления определения истинности высказывания по истинности предпосылок. С развитием релейных и других систем на переключательных элементах алгебра высказываний стала развиваться как сугубо прикладная наука.

Оказалось, что системы на переключательных элементах хорошо описываются уравнениями булевой алгебры. Сейчас алгебра логики - это мощное средство проектирования средств вычислительной техники.

Высказывание - это повествовательное предложение, относительно которого можно определенно сказать, истинно оно или ложно. Например: "Луна - спутник Земли" - истинное высказывание, "Два больше трех" - ложное высказывание. Такие предложения, как "Как вы себя чувствуете?", "Будь внимателен!", не являются высказываниями и в алгебре высказываний не рассматриваются.

Высказывания принято обозначать буквами латинского алфавита. Так, высказывание "Трава — зеленая" можно обозначить буквой А, "Лев – птица" - буквой В и т. д. В алгебре высказываний отвлекаются от конкретного содержания высказывания и интересуются лишь вопросом, является ли оно истинным или ложным.

Каждому верному высказыванию присваивается значение истинности 1 (истина), каждому неверному – значение истинности 0 (ложь). Например, А=1, В=0.

Над высказываниями можно производить логические операции. В результате выполнения операций получаются новые высказывания, истинность которых определяется истинностью исходных высказываний и характером логических операций.

Соединение двух высказываний союзом И называется логическим умножением или конъюнкцией. Эта операция обозначается знаками:

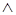" ", "•", "&" или отсутствием знака, например A 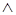B = A•B = A & B = AB. Сложное высказывание АВ считается истинным только в том случае, если истинны оба входящих в него простых высказывания A и В. Истинность конъюнкции определяется табл. 4. Результат конъюнкции легко обобщается на любое число исходных высказываний.

Аппаратно конъюнкция реализуется схемой совпадения (логической схемой И). На выходе схемы совпадения единичный сигнал присутствует только при одновременном наличии единичных сигналов на всех входах схемы.

Соединение двух высказываний союзом ИЛИ называется логическим сложением, или дизъюнкцией. Эта операция обозначается знаками: " 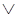", "+". Сложное высказывание A+В считается истинным в том случае, если истинно хотя бы одно из входящих в него простых высказываний А и В. Истинность дизъюнкции определяется табл. 4. Результат дизъюнкции легко обобщается на любое число исходных высказываний.

Аппаратно дизъюнкция реализуется схемой сборки (логической схемой ИЛИ). На выходе схемы сборки единичный сигнал присутствует при наличии хотя бы одного единичного сигнала на входах схемы.

Присоединение частицы НЕ к высказыванию А называется отрицаниемили инверсией. Эта операция обозначается ⌐­А,или 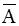(читается: не А). Если высказывание истинно, то его отрицание ложно, и наоборот. Инверсия определяется табл. 4.

Аппаратно инверсия реализуется схемой инвертора (логической схемой НЕ). На выходе инвертора единичный сигнал присутствует при отсутствии единичного сигнала на входе.

Таблица 4 Таблица истинности основных логических операций

Конъюнкция	Дизъюнкция	Инверсия
А	В	АВ	А	В	А+В	А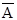

Свойства логических операций:

АВ = ВА коммутативность; (1)

А+В = В+А коммутативность; (2)

(АВ)С = А(ВС) ассоциативность; (3)

А+(В+С) = (А+В)+С ассоциативность; (4)

АА = А идемпотентность; (5)

А+А = А идемпотентность; (6)

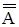= А двойное отрицание; (7)

A0 = 0 свойство конъюнкции Таб.4.1

A1 = A свойство конъюнкции Таб.4.1

A+1 = 1 свойство дизъюнкции Таб.4.2

A(B+C) = АВ+АС дистрибутивность; (8)

А+ВС = (А+В)(A+С) дистрибутивность; (9)

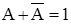исключение третьего; (10)

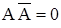противоречие; (11)

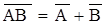закон де Моргана (12)

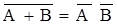закон де Моргана (13)

Свойства логических операций доказываются с помощью сравнения таблиц истинности, соответствующих высказываниям левой и правой частей логических выражений.

При доказательстве свойств логических операций сложные выражения приводят к более простому виду.

Пример. Докажем свойство дистрибутивности функций:

(А+В)(А+С) = А+ВС

Перемножая сомножители левой части равенства как многочлены (сначала (А+ В) на А, а потом (А+В) на С), получаем:

AA+AB+AC+BC = (A+AB+AC)+BC = A(1+В+C)+BC.

Выражение (1+В+C) = 1 (свойство дизъюнкции). Следовательно:

A(1+В+С)+BC = A1+BC = A+BC.