Однонаправленные сумматоры

Существует простая функция однонаправленного сумматоры [116] (см. раздел 4.12.):

A(x_i, y) = x_i-1^y mod n

Числа n(являющееся произведением двух простых чисел) и x₀ должны быть заранее согласованы. Тогда суммированием y₁, y₂ и y₃ будет

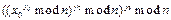
Это вычисление не зависит от порядка y₁, y₂ и y₃.

Раскрытие секретов "все или ничего"

Этот протокол позволяет нескольким сторонам (для работы протокола нужно не меньше двух участников) покупать различные секреты у одного продавца (см. раздел 4.13) [1374, 1175]. Начнем с определения. Возьмем две строки битов, x и y. Фиксированным битовым индексом (fixed bit index,FBI) x и yназывается последовательность номеров совпадающих битов этих строк.

Например:

x= 110101001011

y = 101010000110

FBI(x, y)= {1, 4, 5, 11}

(Мы читаем биты справа налево, считая нулевым крайний правый бит.)

Теперь вот как выглядит протокол. Алиса будет продавцом. Боб и Кэрол - покупателями. У Алисы есть kn-битовых секретов: S₁, S₂, . . . S_k. Боб хочет купить секрет S_b, Кэрол - секрет S_c.

(1) Алиса генерирует пару "открытый ключ/закрытый ключ"и сообщает Бобу (но не Кэрол) открытый ключ. Она генерирует другую пару "открытый ключ/закрытый ключ"и сообщает Кэрол (но не Бобу) открытый ключ.

(2) Боб генерирует kn-битовых случайных чисел, B₁, B₂, . . . B_k, и сообщает их Кэрол. Кэрол генерирует kn-битовых случайных чисел, C₁, C₂, . . . C_k, и сообщает их Бобу.

(3) Боб шифрует C_b(напомним, он хочет купить секрет S_b) открытым ключом, полученным от Алисы. Он вычисляет FBI для C_b и только что зашифрованного результата. Он посылает этот FBI Кэрол.

Кэрол шифрует B_c(напомним, она хочет купить секрет S_c) открытым ключом, полученным от Алисы. Она вычисляет FBI для B_cи только что зашифрованного результата. Она посылает этот FBI Бобу.

(4) Боб берет каждое из n-битовых чисел B₁, B₂, . . . B_kи заменяет каждый бит, номера которого нет в FBI, полученном от Кэрол, его дополнением. Он посылает этот новый список n-битовых чисел B'₁, B'₂, . . . B'_kАлисе.

Кэрол берет каждое из n-битовых чисел C₁, C₂, . . . C_k и заменяет каждый бит, номера которого нет в FBI, полученном от Боба, его дополнением. Она посылает этот новый список n-битовых чисел C'₁, C'₂, . . . C'_k Алисе.

(5) Алиса расшифровывает все C'_iзакрытым ключом Боба, получая kn-битовых чисел C"₁, C"₂, . . . C"_k. Она вычисляет S_iÅC"_i для i= 1, . . . k, и посылает результаты Бобу.

Алиса расшифровывает все B'_iзакрытым ключом Кэрол, получая kn-битовых чисел B"₁, B"₂, . . . B"_k. Она вычисляет S_iÅB"_i для i= 1, . . . k, и посылает результаты Кэрол.

(6) Боб вычисляет S_b, выполняя XOR C_bи b-го числа, полученного от Алисы.

Кэрол вычисляет S_c, выполняя XOR B_cи c-го числа, полученного от Алисы..

Все так сложно. Поясним эти долгие действия на примере.

У Алисы есть для продажи восемь 12-битовых секретов: S₁= 1990, S₂= 471, S₃= 3860, S₄= 1487, S₅= 2235, S₆= 3751, S₇= 2546 и S₈= 4043. Боб хочет купить S₇, а Кэрол - S₂.

(1) Алиса использует алгоритм RSA. В диалоге с Бобом она использует следующую пару ключей: n= 7387, e = 5145 и d= 777, а в диалоге с Кэрол - n= 2747, e= 1421 и d= 2261. Она сообщает Бобу и Кэрол их открытые ключи.

(2) Боб генерирует восемь 12-битовых чисел, B₁= 743, B₂= 1988, B₃= 4001, B₄= 2942, B₅= 3421, B₆= 2210, B₇=2306 и B₈= 222, и сообщает их Кэрол. Кэрол генерирует восемь 12-битовых чисел, C₁= 1708, C₂ = 711, C₃= 1969, C₄= 3112, C₅ = 4014, C₆= 2308, C₇ = 2212 и C₈= 222, и сообщает их Бобу.

(3) Боб хочет купить S₇, поэтому он открытым ключом, выданным Алисой, шифрует C₇.

2212⁵¹⁴⁵ mod 7387 = 5928

Теперь:

2212 = 0100010100100

5928 = 1011100101000

Следовательно, FBI этих двух чисел равен {0, 1, 4, 5, 6}. Он посылает его Кэрол.

Кэрол хочет купить S₂, поэтому она открытым ключом, выданным Алисой, шифрует B₂ и вычисляет FBI B₂ и результата шифрования. Она посылает Бобу{0, 1, 2, 6, 9, 10}.

(4) Боб берет B₁, B₂, . . . B₈и заменяет каждый бит, индекс которого отсутствует в наборе {0, 1, 2, 6, 9, 10} его дополнением. Например:

B₂= 111111000100 = 1988

B'₂ = 011001111100 = 1660

Он посылает B'₁, B'₂, . . . B'₈Алисе.

Кэрол берет C₁, C₂, . . . C₈и заменяет каждый бит, индекс которого отсутствует в наборе {0, 1, 4, 5, 6}его дополнением. Например:

C₇ = 0100010100100 = 2212

C'₇= 1011100101000 = 5928

Она посылает C'₁, C'₂, . . . C'₈Алисе.

(5) Алиса расшифровывает все C'_iзакрытым ключом Боба и выполняет XOR результатов с S_i. Например, для i= 7:

5928⁷⁷⁷ mod 7387 = 2212; 2546 Å2212 = 342

Она посылает результат Бобу.

Алиса расшифровывает все B'_iзакрытым ключом Кэрол и выполняет XOR результатов с S_i. Например, для i= 2:

1660²²⁶¹ (mod 2747) = 1988; 471 Å 1988 = 1555

Она посылает результат Кэрол.

(6) Боб вычисляет S₇, выполняя XOR C₇и седьмого числа, полученного им от Алисы:

2212 Å 342=2546

Кэрол вычисляет S₂, выполняя XOR B₂ и второго числа, полученного ей от Алисы.

1988 Å 1555 = 471

Протокол работает для любого количества покупателей. Если Боб, Кэрол и Дэйв хотят купить секреты, Алиса выдает каждому покупателю два открытых ключа, по одному на каждого другого покупателя. Каждый покупатель получает набор чисел от каждого другого покупателя. Затем они выполняют протокол с Алисой для каждого из своих наборов номеров и выполняют XOR всех полученных от Алисы результатов, получая свои секреты. Более подробно это описано в [1374, 1175].

К сожалению, пара нечестных участников могут смошенничать. Алиса и Кэрол, действуя на пару, могут легко понять, какой секрет получил Боб: если они знают FBI C_b и алгоритм шифрования Боба, они могут подыскать такое b, что у C_bбудет правильный FBI. А Боб и Кэрол, действуя вместе, могут легко заполучить все секреты Алисы.

Если вы считаете, что участники честны, можно использовать протокол попроще [389].

(1) Алиса шифрует все секреты RSA и посылает их Бобу:

C_i= S_i^emod n

(2) Боб выбирает свой секрет C_b, генерирует случайное число r и посылает Алисе.

C'= C_br^emod n

(3) Алиса посылает Бобу^

P'= C'^dmod n

(4) Боб вычисляетP'

S_b= P'r^-1 mod n

Если участники могут жульничать, Боб может доказать с нулевым знанием, что он знает некоторое r, такое что C'= C_br^emod n, и хранить в bсекрете, пока Алиса не передаст ему на этапе (3) P' [246).