Понятия сложности и эффективности алгоритмов и структур данных

В процессе решения прикладных задач выбор подходящего алгоритма вызывает определенные трудности. Алгоритм должен удовлетворять следующим противоречащим друг другу требованиям:

1) быть простым для понимания, перевода в программный код и отладки;

2) эффективно использовать вычислительные ресурсы и выполняться по возможности быстро.

Если разрабатываемая программа, реализующая некоторый алгоритм, должна выполняться только несколько раз, то первое требование наиболее важно. В этом случае стоимость программы оптимизируется по стоимости написания (а не выполнения) программы. Если решение задачи требует значительных вычислительных затрат, то стоимость выполнения программы может превысить стоимость написания программы, особенно если программа выполняется многократно. Поэтому, более предпочтительным может стать сложный комплексный алгоритм (в надежде, что результирующая программа будет выполняться существенно быстрее). Таким образом, прежде чем принимать решение об использовании того или иного алгоритма, необходимо оценить сложность и эффективность этого алгоритма.

Сложность алгоритма – это величина, отражающая порядок величины требуемого ресурса (времени или дополнительной памяти) в зависимости от размерности задачи.

Таким образом, будем различать временную T(n) и пространственную (её также называют ёмкостной) V(n) сложности алгоритма. При рассмотрении оценок сложности, будем использовать только временную сложность. Пространственная сложность оценивается аналогично.

Самый простой способ оценки – экспериментальный, то есть запрограммировать алгоритм и выполнить полученную программу на нескольких задачах, оценивая время выполнения программ. Однако, этот способ имеет ряд недостатков. Во-первых, экспериментальное программирование – это, возможно, дорогостоящий процесс. Во-вторых, необходимо учитывать, что на время выполнения программ влияют следующие факторы:

1) временная сложность алгоритма программы;

2) качество скомпилированного кода исполняемой программы в силу различий в реализации отдельных операторов языка высокого уровня с учетом «оптимизации» компилятора под конкретный процессор;

3) внешние задержки, вызванные работой операционной системы, например, при реализации механизма многозадачности или других программ, работающих в «фоновом» режиме (например, антивирусы);

4) машинные инструкции, используемые для выполнения программы, которые ориентированы на аппаратные особенности архитектуры ЭВМ, например, параллельную обработку линейной последовательности данных.

Наличие трех последних факторов не позволяет применять типовые единицы измерения временной сложности алгоритма (секунды, миллисекунды и т.п.), так как можно получить самые различные оценки для одного и того же алгоритма, если использовать труд разных программистов (которые реализуют алгоритм каждый по-своему), разные компиляторы, операционные системы и разные вычислительные машины.

Таким образом, будем различать время выполнения программы, которое можно измерить в секундах (миллисекундах, аппаратных тактах центрального процессора) и время выполнения соответствующего ей алгоритма, которое будем измерять числом инструкций (элементарных или основных операций), которые необходимо выполнить для получения требуемого результата.

Существует метод, позволяющий теоретически оценить время выполнения алгоритма, который и рассмотрим далее. Однако, рассматриваемый подход следует использовать аккуратно, так как он не учитывает количество выполняемых алгоритмом операций, не относящихся к основным. Кроме того, это значение можно определить только приблизительно.

Часто, временная сложность алгоритма зависит от количества входных данных. Обычно говорят, что временная сложность алгоритма имеет порядок T(n) от входных данных размера n. Точно определить величину T(n) на практике представляется довольно трудно. Поэтому прибегают к асимптотическим отношениям с использованием O-символики, которая дает приемлемую оценку времени выполнения алгоритма для не бесконечно больших и не бесконечно малых значений n. Она также позволяет ответить на вопросы наподобие: «во сколько раз быстрее будет работать реализация данного алгоритма на компьютере, быстродействие которого больше нашего, например, в 10 раз»? Казалось бы, ответ очевиден — в 10 раз. Однако, если O(n) = n(n + 1)/2, то это далеко не так. Или: «насколько дольше будет выполняться программа, если удвоить размер входных данных»? Ответ будет такой: приблизительно в четыре раза медленнее.

Когда используют обозначение «O(×)», имеют в виду не точное время исполнения, а только его предел сверху, причем с точностью до постоянного множителя. Когда говорят, например, что алгоритму требуется время порядка O(n²), имеют в виду, что время исполнения задачи растет не быстрее, чем квадрат количества элементов.

Например, если число тактов (действий), необходимое для работы алгоритма, выражается как 25n² – 10n*log n + 5n + 15, то это алгоритм, для которого T(n) имеет порядок O(n²). Фактически, из всех слагаемых оставляется только то, которое вносит наибольший вклад при больших n (в этом случае остальными слагаемыми можно пренебречь), и игнорируется коэффициент перед ним.

Говоря нестрого, обозначение 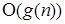– это множество всех функций, порядок роста которых при достаточно больших n не превышает (т.е. меньше или равен) некоторую константу, умноженную на значение функции .

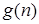Практически время выполнения алгоритма зависит не только от количества входных данных, но и от их значений, например, время работы некоторых алгоритмов сортировки значительно сокращается, если первоначально данные частично упорядочены, тогда как другие методы оказываются нечувствительными к этому свойству. Чтобы учитывать этот факт, полностью сохраняя при этом возможность анализировать алгоритмы независимо от данных, различают:

1. максимальную сложность T_max(n), или сложность наиболее неблагоприятного случая, когда алгоритм работает дольше всего;

2. среднюю сложность T_mid(n) – сложность алгоритма в среднем;

3. минимальную сложность T_min(n) – сложность в наиболее благоприятном случае, когда алгоритм справляется быстрее всего.