Свойства асимптотических функций
Введённые нами определения обладают некоторыми свойствами транзитивности, рефлексивности и симметричности.
Транзитивность:
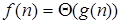 и
и 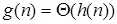 влечёт
влечёт 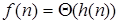 ;
;
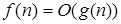 и
и 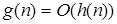 влечёт
влечёт 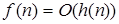 ;
;
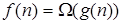 и
и 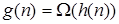 влечёт
влечёт 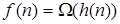 ;
;
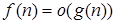 и
и 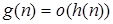 влечёт
влечёт 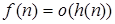 ;
;
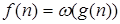 и
и 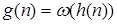 влечёт
влечёт 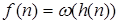 .
.
Рефлексивность:
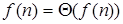 ,
, 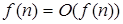 ,
, 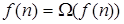 .
.
Симметричность:
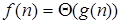 если и только если
если и только если 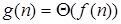 .
.
Обращение:
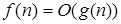 если и только если
если и только если 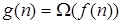 ;
;
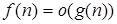 если и только если
если и только если 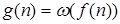 .
.
Можно провести весьма условную параллель: отношения между функциями f и g подобны отношениям между числами a и b:
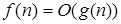 ≈
≈ 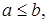
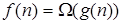 ≈
≈ 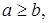
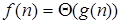 ≈
≈ 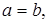
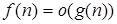 ≈
≈ 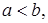
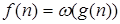 ≈
≈ 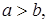
Замечание. Следует осторожно использовать формулы при работе с О-символикой. Например, формулу 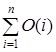 ошибочно трактовать по правилу суммы
ошибочно трактовать по правилу суммы
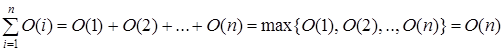 ,
,
т.к. число последовательных фрагментов есть сама функция от n.
Если операция выполняется за фиксированное число шагов, не зависящее от количества данных, то принято писать O(1).
Пример 1: пусть мы смогли определить величины T(0) = 1, Т(1) = 4, Т(2) = 9 или в общем случае T(n) = (n + 1)². Требуется найти асимптотическую оценку О(f(n)), т.е. некоторую функцию вида f(n), которая бы относилась к одному из известных классов сложности алгоритмов и график которой располагался бы над графиком функции экспериментальных значений времени выполнения программы T(n), то есть описывал зависимость числа выполненных инструкций в худшем случае.
Решение: Как известно, (n + 1)2 = n2 + 2n + 1, то есть T(n) = n2 + 2n + 1.
| В качестве асимптотической оценки, т.е. функции расположенной над T(n) можно взять функцию вида f’(n) = n3, так как n3 > n2 + 2n + 1, однако тем самым мы ухудшим «мнение» эксперта об исследуемом алгоритме (он работает быстрее), так как если положить f(n) = n2, и найти такую константу с, чтобы выполнилось T(n) ≤ n2 * с. При с = 2, начиная с n0 = 3, исключая случаи запуска программы с длиной входных данных 1 и 2. Разрешая неравенство 2n2 ≥ n2 + 2n + 1 относительно n, получаем n0 = 3. | 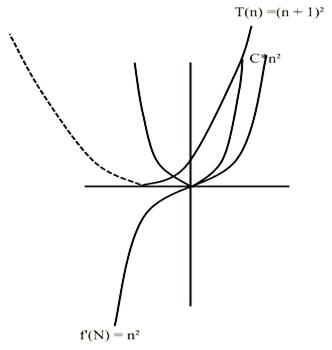 Рис. 4 Определение константы с и n0
Рис. 4 Определение константы с и n0
|
Заметим, что при с= 3 → n0 = 2, что лучше чем при с= 3, так как асимптотическая оценка справедлива на большем диапазоне входных данных. Самый «идеальный» случай, когда функция f(n) превышает T(n) на всем наборе исходных данных n ≥ 1 – это условие выполняется при с = 4 и n0 = 1.
В отличие от примера T(n) как функцию от некоторого аргумента аналитически задать сложно, а в большинстве случаев – невозможно. Единственный выход – найти верхнюю и нижнюю асимптотическую оценку характера изменения T(n). Для чего вводиться функция Ω(f(n)), которая представляет нижнюю асимптотику. Тогда надо подобрать такой вид функции роста (то есть полином f(n)) для О(f(n)) и Ω(f(n)), что они совпадут в обоих случаях с точностью до полинома – тогда получим точную асимптотическую оценку Θ(f(n))функции T(n). Согласно определению Θ(×)
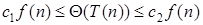 .
.
Не трудно заметить, что условие
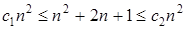
выполняется при с1 = 1 и с2 = 4 на всем множестве n. Поэтому для полинома 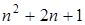 точная асимптотическая оценка составляет n2.
точная асимптотическая оценка составляет n2.
Поскольку для f(n) = n3 имеет строгое неравенство n3 > n2 + 2n + 1, то f(n) = n3 есть o(×), то есть о(T(n)) = n3.
Пример 2. По экспериментальным данным T(n) замеров времени выполнения (числа фактически выполненных инструкций) некоторой программы эмпирически определить характер функции роста трудоемкости реализованного алгоритма, вид и значения её асимптотической оценки Θ(n), O(n), o(n), W(n), ω(n):
| n | |||||||||||||||
| T(n) |
Решение. Будем решать поставленную задачу графическим методом, то есть построив график T(n), будем подбирать функции, описывающие соответствующий класс сложности алгоритмов. Построив соответствующие графики, наглядно покажем выполнения требований, согласно определениям Θ(n), O(n), o(n), W(n), ω(n).
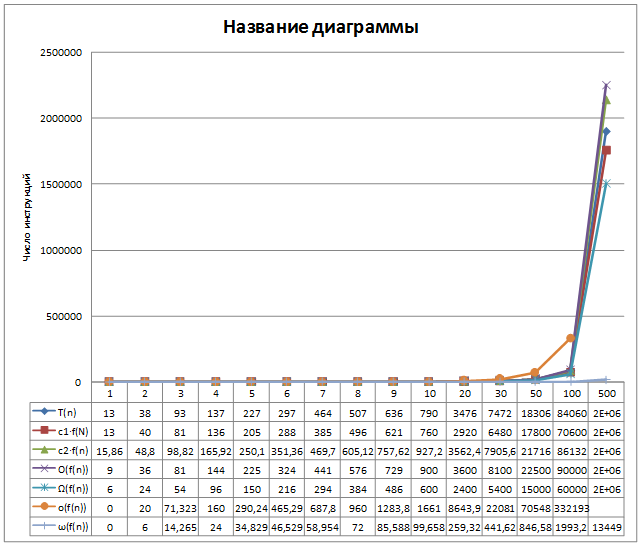
Рис. 5 Графическое и табличное представления решения задачи.
Как видно из графиков, наилучшим приближением к экспериментальным значениям T(n) будет функция роста, описываемая полиномом вида 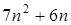 . Действительно, согласно определению Θ(n) необходимо выполнение требования
. Действительно, согласно определению Θ(n) необходимо выполнение требования 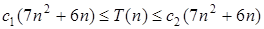 и при
и при 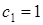 ,
, 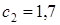 и
и 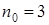 условие выполняется (на графике через c1f(n) и c2f(n) обозначены асимптотические границы согласно определению Θ(n) и рис. 2.). Поэтому можно утверждать, что
условие выполняется (на графике через c1f(n) и c2f(n) обозначены асимптотические границы согласно определению Θ(n) и рис. 2.). Поэтому можно утверждать, что 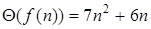 .
.
Графики и таблица подтверждают, что
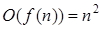 при
при 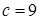 и
и 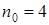 ;
;
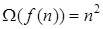 при
при 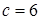 и
и 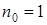 ;
;
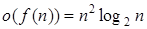 при
при 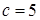 и
и 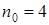 ;
;
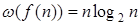 при
при 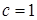 и
и 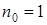 .
.
Дата добавления: 2022-02-05; просмотров: 418;











