Числові характеристики ННВ

Означення. Математичним сподіванням неперервної випадковоївеличини Х, заданої щільністю розподілу 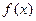, називається число, яке обчислюється за формулою

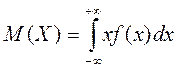
Якщо неперервна випадкова величина приймає значення на відрізку [a;b] та має щільність ймовірностей 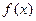, то її математичне сподівання знаходиться за формулою

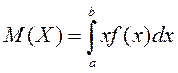
Задача 5. Випадкова величина задана щільністю розподілу

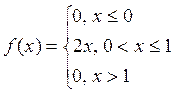
Знайти математичне сподівання.

Розв’язання. .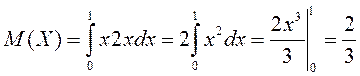

Відповідь:.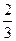

Для неперервної випадкової величини дисперсія обчислюється за формулою:

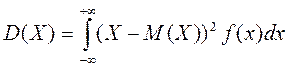(17)

або

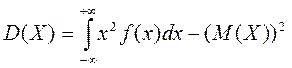(18)

Задача 6.Випадкова величина задана щільністю розподілу

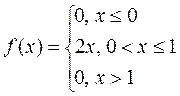
Знайти дисперсію та середнє квадратичне відхилення.

Розв’язанняУ задачі 5 знайдено математичне сподівання .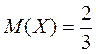

М(Х²)= 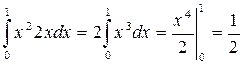. За формулою (18) знаходимо дисперсію

.

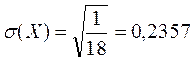Відповідь: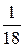, 0,2357.

Правило трьох сигм

Якщо випадкова величина Х розподілена нормально, то 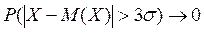, тобто ймовірність того, що абсолютна величина відхилення Х від її математичного сподівання прямує до нуля, а це означає, що 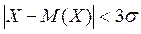– практично достовірна подія.

У практиці це правило використовують так: якщо закон розподілу випадкової величини Х невідомий, але 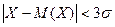, тоді можна припустити, що Х розподілена нормально.