Алгоритмически неразрешимые проблемы.
Тьюрингом был выдвинут тезис: каждый алгоритм может быть реализован с помощью машины Тьюринга. Это даёт точное определение алгоритма, которое может быть использовано для доказательства алгоритмической неразрешимости ряда проблем.
Как ранее указывалось, при соответствующей кодировке задачи можно считать функциями, определёнными на неотрицательных целых числах и принимающими такие же значения. Приняв тезис Тьюринга, получаем, что алгоритмически разрешимым задачам соответствуют вычислимые на МТ функции.
Существование алгоритмически неразрешимых проблем можно усмотреть уже из мощностных соображений, так различных МТ – счетное число, а функций - значительно больше. В самом деле, имеется конечное число МТ с m + 1 внутренними состояниями и внешним алфавитом из заданных n + 1 символов, а именно, не более [3(m+1)(n+1)](m+1)(n+1) поэтому всех МТ – счётное число. В то же время даже функций вида f: N → {0,1} имеется более чем счётное число, так как каждую такую функцию можно рассматривать как характеристическую функцию некоторого подмножества натуральных чисел, а множество подмножеств всегда имеет мощность, большую мощности самого множества.
На языке МТ можно указать и содержательные неразрешимые проблемы. Рассмотрим алгоритмическую проблему самоприменимости, состоящую в следующем. Так как всех МТ – счётное число, то множество МТ можно закодировать, присвоив каждой МТ в качестве идентифицирующего кода натуральное число n (m). При этом всё множество МТ разобьётся на 2 класса: МТ, применяемых к собственному номеру, т.е. к слову 1n(m), и неприменимых. Назовём МТ первого класса самоприменимыми, а второго – несамоприменимыми.
Некоторая МТ решает проблему самоприменимости, если по коду произвольной машины она определяет, самоприменима она или нет. Докажем, что такой МТ не существует. Допустим противное. Пусть такая МТ имеется и на коде самоприменимой машины она завершает работу в конфигурации ...q0 1... , а на коде несамоприменимой - ...q0 0... . Тогда, сделав незначительные изменения в программе, легко добиться того, чтобы МТ останавливалась на кодах несамоприменимых машин и не останавливалась на кодах самоприменимых машин.
Для этого считаем, что состояние q0 не заключительное состояние, а в качестве в качестве заключительного введем новое состояние 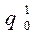 и добавим в программу МТ две новые команды:
и добавим в программу МТ две новые команды:
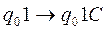
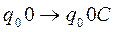
Зададимся теперь вопросом, применима ли эта МТ к своему собственному коду. Если применима, то она применима к коду самоприменимой машины, а это невозможно. Полученное противоречие и является доказательством алгоритмической неразрешимости проблемы самоприменимости.
Теперь можно рассмотреть и более содержательную проблему применимости данной МТ к заданному слову Р. Допустим, что существует МТ, которая по коду n(M) и слову Р решает, применима ли данная машина к слову Р. Тогда, если в качестве слова Р взять код машины n(M), то наша МТ будет решать проблему самоприменимости, а это невозможно. Поэтому проблема алгоритмически неразрешима.
Контрольные вопросы.
1. Дайте определение понятия «алгоритм».
2. Опишите суть алгоритма Евклида для нахождения наибольшего общего делителя двух многочленов.
3. Что будет, если с помощью алгоритма Евклида находить общую меру стороны и диагонали квадрата?
4. Опишите суть модели алгоритма, называемой машиной Тьюринга.
5. Что называется конфигурацией?
6. Что значит, что машина Тьюринга применима к данному слову?
7. Какие алгоритмически неразрешимые проблемы вы знаете?
Тест V
1) Для нахождения (48,27) алгоритма Евклида выполнит
а) 2 шага; б) 3 шага; в) 4 шага.
2) Наибольший общий делитель многочленов x2-3x+2 и x2-4x+3 равен
а) x+1; б) x-1; в) x2-1.
3) Применима ли к слову 1100 машина Тьюринга, задаваемая программой
q11 → q10R
q10 → q21L
q21 → q01C
q20 → q10R
а) применима; б) не применима.
4) Корнями уравнения 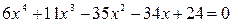 являются числа
являются числа
а) 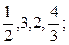 б)
б) 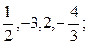 в)
в) 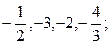 г)
г) 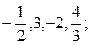
5) Среди трех монет одна фальшивая. В результате какого наименьшего числа взвешиваний можно определить фальшивую монету
а) одного; б) двух; в) трех.
Дата добавления: 2022-02-05; просмотров: 629;











