Глава 5. Алгоритмы и машина Тьюринга.

5.1. Понятие алгоритма.

Алгоритм- это точное предписание, задающее процесс решения задачи. Алгоритм задаётся набором инструкций, последовательные выполнения которых являются элементарными шагами алгоритма. Процесс начинается с исходных данных, выделяющих данную индивидуальную задачу из множества задач, решаемых алгоритмом, и направлен на получение полностью определяемого этими исходными данными результата. Примерами алгоритмов являются изучаемые в школе правила сложения, вычитания, умножения и деления столбиком. Здесь исходными данными служат упорядоченные пары натуральных чисел, записанные в десятичной системе, а результатом - также натуральное число в десятичной системе. Само слово алгоритм происходит от имени среднеазиатского математика Мухаммеда бен Мусы аль – Хорезми, давшего в 825 году правила выполнения 4 арифметических действий в десятичной системе. Понятие алгоритма является одним из важнейших в современной математике. С появлением вычислительных машин понятие алгоритма тесно связано с программированием, так как программа на ЭВМ является формой представления алгоритма на некотором алгоритмическом языке программирования.

Теория алгоритмов в настоящее время – это обширная область математики. Одним из важнейших вопросов в ней является вопрос алгоритмической разрешимости определённого класса задач. Были найдены классы задач, для решения которых не существует алгоритма, так называемые алгоритмически неразрешимые проблемы.

Пусть, например, требуется установить, имеет ли целые корни данное алгебраическое уравнение

а₀ xⁿ + а₁ x^n-1 +…+ а_n-1 x + а_n =0

с целым коэффициентами a₀, a₁,...,a_n.

Алгоритм для решения этой задачи существует, так как если это уравнение имеет целый корень р, то р должно быть делителем числа a_n. Поэтому для данного уравнения можно найти все делители числа a_n и все по очереди проверить. Однако, аналогичная проблема для уравнений P(x₁,...,x_m)=0, где P(x₁,...,x_m) – произвольный многочлен с целыми коэффициентами от любого числа m неизвестных, оказалась алгоритмически неразрешимый. Получение подобных результатов, относящихся к неразрешимости определённого класса задач, потребовало уточнения понятия алгоритма. Одним из возможных и используемых в математике подобных уточнений является рассматриваемая далее машина Тьюринга.

В тех же случаях, когда сама разрешимость не вызывает сомнений, центральным в теории алгоритмов становится вопрос трудоёмкости решения, т.е. оценка числа элементарных операций, выполняемых алгоритмом при решении задачи. Пусть U – множество решаемых задач, А – множество алгоритмов, решающих задачи данного класса, N (a,u) – число элементарных операций, выполняемых алгоритмом aÎA при решении задачи uÎU. Тогда в качестве эффективности алгоритма а можно взять число операций на самой трудной для него задаче из данного класса 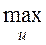N (a,u). Если теперь выбрать из множества возможных алгоритмов алгоритм, для которого эта величина принимает минимальное значение, то получиться величина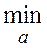 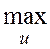N (a,u), которая уже не зависит ни от u, ни от а, а характеризует трудоёмкость задач класса U в целом.

На самом деле класс решаемых задач U состоит, как правило, из однотипных задач различной размерности, и трудоёмкость решения индивидуальной задачи в значительной степени определяется её размерностью. Так, трудоёмкость выполнения арифметических действий зависит от величины участвующих в них чисел. Поэтому задачи класса U разбиваются на подклассы по размерности задач, и трудоёмкость определяется для каждого из подклассов как функция размерности. Скорость роста этой функции и характеризует сложность решения задач данного класса.

Рассмотрим эти понятия на примере простого, но чрезвычайно важного как с теоретической, так и с практической точек зрения алгоритма Евклида для нахождения наибольшего общего делителя двух натуральных чисел.

5.2. Алгоритм Евклида.

Пусть даны два натуральных числа n и m, причём n ³ m. Требуется найти их наибольший общий делитель d = (n, m). Способ для решения этой задачи, приведённый в книге Начала Евклида, состоит в следующем. Делим число n на m с остатком. Это даёт n = k₁m + r₁, где частное k₁ является целым положительным числом, а остаток r₁ – либо 0, либо положительное число, меньше m, 0£ r₁<m. Если остаток не равен нулю, то повторяем операцию деления с остатком, но делимым является делитель предыдущего шага, а делителем – его остаток, и так до тех пор, пока не получиться остаток, равный нулю. Последний, положительный остаток в этом процессе и является наибольшим общим делителем чисел n и m. Процесс может быть описан следующей цепочкой равенств:

n = k₁m + r₁

m = k₂ r₁ + r₂

r₁ = k₃ r₂ + r₃

r₂ = k₄ r₃ + r₄

¼¼¼¼¼¼

r_l-4 = k_l-2 r_l-3 + r_l-2

r_l-3 = k_l-1 r_l-2 + r_l-1

r_l-2 = k_l r_l-1

r_l-1 = (n, m)

Компактно алгоритм Евклида может быть представлен следующей блок-схемой:

Начало

n, m

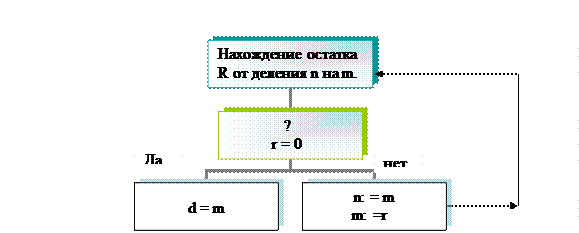
Конец

(n, m) = d

Циклически повторяемая операция деления с остатком является фактически единственной операцией этого алгоритма. Поэтому число её повторений может служить естественной мерой трудоёмкости алгоритма Евклида.

Так как r₁ < n/2, то делимое за 2 шага уменьшается более чем вдвое. Поэтому число шагов алгоритма l может быть оценено сверху как

l < 2 log₂ n. Если число n представлена в десятичной системе исчисления, то, как показывает данная оценка, число шагов ограничено линейной функцией от длины записи числа n. Поэтому алгоритм Евклида очень эффективный алгоритм. Намного более трудоёмким было бы нахождение наибольшего общего делителя с помощью разложения чисел m и n на простые множители.

Алгоритм Евклида можно применять также для нахождения наибольшего общего делителя двух многочленов и общей меры двух соизмеримых отрезков. Если отрезки несоизмеримы, т.е. их отношение выражается иррациональным числом как, например, у стороны квадрата и его диагонали, то алгоритм Евклида приводит к бесконечному процессу.

Для обоснования алгоритма Евклида достаточно заметить, что из равенства n = k₁m + r₁ вытекает, что каждый делитель чисел m и n является делителем чисел m и r₁ и наоборот, следовательно (n, m) = (m, r₁).

Поэтому суть алгоритма Евклида в том, он сводит задачу нахождения наибольшего общего делителя двух чисел к аналогичной задаче для меньших чисел.

Из алгоритма Евклида можно сделать ещё один чрезвычайно важный вывод, а именно, (m, n) выражается линейно через m и n:

(m, n) = sn + tm, где s и t – целые числа.

В самом деле, из первого равенства цепочки получаем r₁ = n – k₁m, т.е. r₁ линейно зависит от n и m. Из второго равенства r₂ = m – k₂ r₁, т.е. r₂ линейно зависит от m и r₁, но r₁ линейно зависит от n и m, поэтому r₂ также линейно зависит от n и m:

r₂ = m – k₂ (n – k₁m) = (k₁ k₂ + 1)m - k₂ n. продолжая движение по цепочке, окончательно получаем, что наибольший общий делитель двух чисел линейно с целыми коэффициентами через них выражается.

В заключение приведём численный пример использования алгоритма Евклида. Пусть требуется найти наибольший общий делитель чисел 7200 и 3132. Последовательные шаги алгоритма в этом случае таковы:

7200 = 2 * 3132 + 936

3132 = 3 *936 + 324

936 = 2 * 324 + 288

324 = 1 * 288 + 36

288 = 8 *36

(7200, 3132) = 36.

Машина Тьюринга.

Доказательство алгоритмической неразрешимости определённых задач стало возможным после уточнения понятия алгоритма. В первой половине 20 века было предложено несколько таких уточнений, впоследствии оказавшихся эквивалентными. Все они исходят из того, что алгоритм можно рассматривать как отображение из множества описаний задач во множество результатов. Если элементы этих множеств закодировать целыми неотрицательными числами, то алгоритмический процесс представляет собой вычисление некоторой функции, аргументы и значение которой являются целыми неотрицательными числами. Функция называется вычислимой, если её значения могут быть вычислены с помощью алгоритма. Тогда существование невычислимых функций влечёт существование алгоритмически неразрешимых задач.

В 30 – е годы английским математиком Тьюрингом в качестве модели алгоритма было предложено гипотетическое вычислительное устройство, которое в определённой мере оказалось прототипом современных ЭВМ. Теперь его называют машиной Тьюринга (МТ).

МТ имеем конечное множество внутренних состояний Q = {q₀, q₁ ,..., q_m}, где q₁ считается начальным, а q₀ – конечным состояниями, а также внешнюю память в виде ленты, состоящей из конечного числа ячеек, в которых записаны символы из внешнего алфавита A = {a₀, a_{1 ,...,} a_n}, причём символ a₀ считается пустым и обычно обозначается как 0. В процессе работы МТ к существующим ячейкам могут пристраиваться новые пустые ячейки, так что лента является потенциально неограниченной в обе стороны.

В каждый из дискретных моментов времени МТ находится в одном из своих внутренних состояний и обозревает одну из ячеек ленты, воспринимая записанный в ней символ. В зависимости от внутреннего состояния и воспринимаемого символа в следующий момент МТ переходит в новое внутреннее состояние (возможно, то же самое), записывает новый символ в обозреваемую ячейку (возможно, тот же самый) и начинает обозревать соседнюю ячейку слева, либо ту же самую ячейку, либо соседнюю ячейку справа. Таким образом, функционирование МТ задаётся тремя функциями:

G : Q 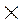A ® Q

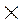F : Q A ® A

D : Q 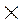A ® {L, C, R}.

Попав в заключительное состояние q₀, МТ прекращает работу.

Функции G, F, и D задаются набором команд или программой для МТ. Команды имеют вид q_i a_j ® q_k a_l s_p, где q_k = G(q_i a_j), a_i = F(q_i a_j), s_p = D(q_i, a_j).

В каждый момент времени состояние МТ полностью определяется внутренним состоянием q_i, содержимым ячеек ленты a_i1, a_i2 ,..., a_it и номером k обозреваемой ячейки, что в совокупности называется конфигурацией и может быть записано как a_i1 a_i2 ,..., a_ik-1

q_i a_ik a_ik+1 ... a_it.

Конфигураций, получающиеся из данной приписыванием слева или справа произвольного числа пустых ячеек, считаются эквивалентными. В процессе работы МТ происходит последовательная смена конфигураций. Начальная конфигурация должна быть задана. Тогда все последующие конфигурации определяются программой. Если условиться считать, что в начальный момент машина находится в состоянии q₁ и обозревает самую левую ячейку ленты, то начальная конфигурация полностью задаётся начальным словом – набором записанных в ячейках ленты символов.

Начав работу с некоторого начального слова, МТ либо остановится через конечное число шагов, либо никогда не остановится. В первом случае говорят, что МТ применима к слову Р, а во втором, - что не применима.

Перейдём к рассмотрению примеров. Будем использовать внешний алфавит из двух символов A = {0, 1}. Если Р – некоторое слово, то для слова P P ...P (m раз) будем для краткости использовать обозначение [P]^m. Так, например, слово 1100011000111 запишется как [1² 0³]² 1³.

Пусть МТ с тремя внутренними состояниями q_0, q₁ и q₂ задаётся программой:

q₁ 0 ® q₁ 0R

q₁ 1 ® q₂ 0R

q₂ 1 ® q₁ 0R

q₂ 0 ® q₀ 1C.

Пусть начальное слово P = 1³ 01. Тогда при работе МТ последовательно возникают конфигурации: q₁ 1³ 01, q₂ 1² 01, q₁ 101, q₂ 01, q₀ 1².

МТ остановилась, перейдя в заключительное состояние q_0, т.е. МТ применима к данному слову.

Пусть теперь начальное слово p = 1⁴. Тогда последовательными конфигурациями будут:

q₁ 1⁴, q₂ 1³, q₁ 1², q₂ 1, q₁ 0, q₁ 0, q₁ 0,… .

МТ никогда не остановится, т.е. МТ не применима к данному слову.

Пусть теперь требуется построить МТ, прибавляющую к данному неотрицательному целому числу единицу, т.е. МТ должна переводить конфигурацию q₁ 1ⁿ в q₀ 1ⁿ⁺¹. Вот такая МТ:

q₁ 1 q₁ 1 R

q₁ 0 q₂ 1 L

q₂ 1 q₂ 1 L

q₂ 0 q₀ 0 R.

Пусть теперь требуется решить задачу удвоения числа, т.е. q₁ 1ⁿ ® q₀ 1²ⁿ. Эта задача может быть решена с помощью такой МТ:

q₁ 1 ® q₂ 0R

q₂ 1 ® q₃ 1 L

q₃ 0 ® q₄ 0 L

q₄ 1 ® q₄ 1 L

q₄ 0 ® q₅ 1R

q₅ 1 ® q₅ 1R

q₅ 0 ® q₁ 1R

q₂ 0 ® q₆ 1 L

q₆ 1 ® q₆ 1 L

q₆ 0 ® q₀ 1C.

Идея алгоритма состоит в том, что в заданном слове 1ⁿ вводится маркерный 0, который в ходе работы алгоритма передвигается слева направо. При каждом его передвижении слева к слову приписывается 1. МТ завершает работу, когда маркерный 0 достигает правого конца исходного слова.