Бинарные алгебраические операции.
Взаимосвязь между матанализом и алгеброй.
В матанализе изучаются, в частности, функции одного и двух аргументов.
Пример 1. 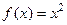 , т.е.
, т.е. 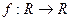
Пример 2. 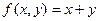 , здесь
, здесь 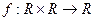
Если множество, на котором задано отображение - не числовая прямая, а какое-то дискретное множество, то применяются алгебраические понятия - унарные и бинарные алгебраические операции (по числу аргументов). Существуют и n-арные операции, например, общий перпендикуляр к трём векторам в 4-мерном пространстве (тогда n=3).
Простейшие примеры. Отображение множества из 3 первых натуральных чисел в само себя. Если в верхней строке записать числа по порядку, а в нижней строке - образ каждого из них, то получится, к примеру, такая запись:
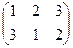
Подстановка.
Впрочем, верхняя строка информации не несёт, можно писать только 2-ю строку, это называется перестановкой. Пример: (3 1 2).
Перестановок 2 порядка всего две: (1 2) и (2 1).
Перестановки 3 порядка:
(1 2 3), (1 3 2) (2 1 3), (2 3 1) (3 1 2), (3 2 1).
Их всего 6. Чтобы перечислить их все, можно на 1 месте поставить число, а на двух других остаётся по 2 варианта расположить оставшиеся 2 числа.
Лемма.Существует n! перестановок порядка n.
Доказательство.
Для n = 2 это очевидно, перестановки только (12) и (21).
Дальше, доказательство по индукции. Пусть теперь для (n-1) этот факт доказан. Рассмотрим для n. На первом месте может стоять любое из n чисел, и при каждой из этих ситуаций, остаётся (n-1) число, которые должны занять (n-1) место, а это возможно (n-1)! способами. Итак, получается 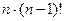 что как раз равно n!, что и требовалось доказать.
что как раз равно n!, что и требовалось доказать.
В частности, при n = 3 получается 6 перестановок:
(123) (132) (213) (231) (312) (321)
На первом месте одно из 3 чисел, и при этом оставшиеся 2 числа можно расставить на 2 места двумя способами. Получается 6 способов. Заметим, что 3! = 6.
Назовём инверсией такую ситуацию, когда большее число в перестановке расположено раньше, чем меньшее. В перестановке (12) инверсий нет, количество инверсий 0, то есть чётно. В перестановке (21) одна инверсия (то есть, их количество нечётно).
Группоид
Определение 1. На множестве 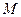 задана бинарная алгебраическая операция, если каждой паре элементов
задана бинарная алгебраическая операция, если каждой паре элементов 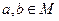 поставлен в соответствие однозначно определённый элемент
поставлен в соответствие однозначно определённый элемент 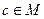 .
.
Примечание. Результат операции также принадлежит М, другими словами, множество замкнуто относительно этой операции.
Это означает, что задано отображение (задана функция) 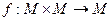 ,
, 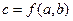 . В матанализе используется функциональные обозначения
. В матанализе используется функциональные обозначения 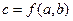 , а в алгебре - знаки алгебраической операции, например
, а в алгебре - знаки алгебраической операции, например 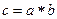 .
.
Граница между матанализом и алгеброй очень тонкая. И та, и другая область математики изучает отображения. В матанализе они называются функциями, здесь - алгебраическими операциями.
Операция, например, может быть сложением или умножением, но не обязательно, на самом деле существует более обширный класс операций, а сложение и умножение - лишь частные случаи.
Определение 2.Если на 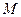 задана бинарная алгебраическая операция, то
задана бинарная алгебраическая операция, то 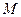 называется группоидом, и обозначается
называется группоидом, и обозначается 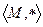 .
.
Примеры.
1. Множество целых чисел с операцией сложения. 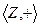 является группоидом, так как результат операции - это снова целое число, то есть операция не выводит за пределы этого множества.
является группоидом, так как результат операции - это снова целое число, то есть операция не выводит за пределы этого множества.
2. Множество целых чисел с операцией умножения. 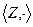 . Аналогично прошлому примеру, является группоидом.
. Аналогично прошлому примеру, является группоидом.
3. 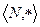 , где
, где 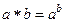 является группоидом. Положительная степень натурального числа есть снова натуральное число.
является группоидом. Положительная степень натурального числа есть снова натуральное число.
4 . Множество натуральных чисел с операцией вычитания. 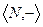 .
. 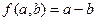 .
.
Не является группоидом, так как эта операция может привести к тому, что результат не принадлежит данному множеству, например, если 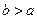 .
.
Свойства операций.
1. Коммутативность.Если для любых 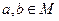 верно
верно 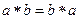 , то операция называется коммутативной, и соответственно, группоид - коммутативным.
, то операция называется коммутативной, и соответственно, группоид - коммутативным.
Примеры.
1. 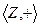 2.
2. 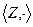 3.
3. 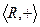 4.
4. 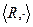 коммутативные группоиды.
коммутативные группоиды.
5. 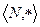 , где
, где 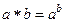 . Не коммутативный группоид. Как минимум,
. Не коммутативный группоид. Как минимум, 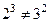 , есть и много других примеров.
, есть и много других примеров.
2. Ассоциативность.Если 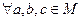 верно
верно 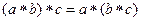 , то операция называется ассоциативной, и соответственно, группоид - ассоциативным (в таком случае его называют полугруппой).
, то операция называется ассоциативной, и соответственно, группоид - ассоциативным (в таком случае его называют полугруппой).
Примеры.
1. 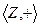 2.
2. 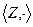 3.
3. 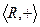 4.
4. 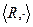 ассоциативные группоиды.
ассоциативные группоиды.
5. 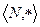 , где
, где 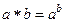 . Не ассоциативный группоид.
. Не ассоциативный группоид.
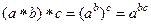
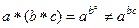 , так как в общем случае
, так как в общем случае 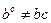 .
.
Нейтральный элемент.
Пусть дан группоид 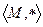 . Если существует такой элемент
. Если существует такой элемент 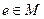 , что
, что 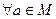 выполняется
выполняется 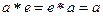 , то
, то 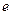 называется нейтральным элементом этого группоида.
называется нейтральным элементом этого группоида.
Пример 1. 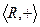 операция сложения, тогда
операция сложения, тогда 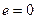 .
.
Пример 2. 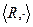 операция умножения, тогда
операция умножения, тогда 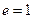 .
.
Нейтральный элемент существует не всегда.
Пример 3. Векторное умножение в пространстве. Если каждой паре векторов ставится в соответствие их общий перпендикуляр, то результат действия операции перпендикулярен каждому из векторов, и невозможна ситуация 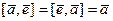 .
.
Пример 4. 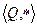 , операция
, операция 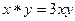 . Тогда
. Тогда 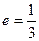 .
. 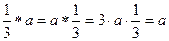 .
.
Лемма.Если существует нейтральный элемент, то он единственный.
Доказательство. Допустим, что существует 2 нейтральных элемента, 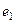 и
и 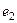 . Если мы умножим их между собой, то должно быть во-первых
. Если мы умножим их между собой, то должно быть во-первых 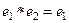 , так как
, так как 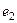 нейтральный, но во-вторых, тогда
нейтральный, но во-вторых, тогда 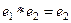 , так как
, так как 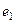 тоже нейтральный. Получается
тоже нейтральный. Получается
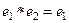 ,
, 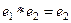 , то есть
, то есть 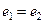 .
.
Симметричный (обратный) элемент
Определение. Пусть группоид 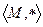 содержит нейтральный элемент
содержит нейтральный элемент 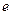 . Элемент
. Элемент 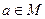 . Элемент
. Элемент 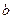 называется симметричным относительно
называется симметричным относительно 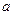 , если
, если 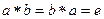 .
.
Примеры.
1. При сложении, в 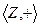 , нейтральный
, нейтральный 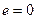 , симметричный это противоположный элемент
, симметричный это противоположный элемент 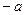 .
.
2. При умножении, в 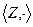 , нейтральный
, нейтральный 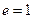 , симметричный это обратный элемент: для
, симметричный это обратный элемент: для 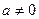 существует
существует 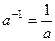 .
.
3. 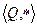 , операция
, операция 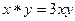 .
. 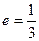 . Обратный равен
. Обратный равен 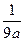 , так как
, так как 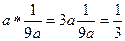 .
.
Лемма. Пусть 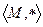 полугруппа (т.е. операция ассоциативна). Тогда, если для элемента
полугруппа (т.е. операция ассоциативна). Тогда, если для элемента 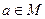 существует симметричный, то он единственный.
существует симметричный, то он единственный.
Доказательство. Пусть для 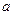 существует 2 разных симметричных элемента,
существует 2 разных симметричных элемента, 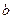 и
и 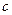 . Тогда
. Тогда
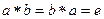 ,
, 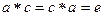 . Рассмотрим равенство
. Рассмотрим равенство 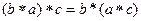 , из него следует, что
, из него следует, что 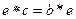 , но тогда
, но тогда 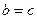 .
.
Пример. Подстановки, нейтральный 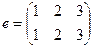
обратный элемент:
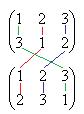
Группы
Определение. Множество 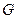 с заданной на нём бинарной операцией
с заданной на нём бинарной операцией 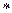 называется группой, если:
называется группой, если:
1) выполняется ассоциативность, т.е.
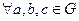
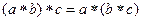
2) существует нейтральный элемент 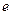 , то есть
, то есть 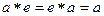
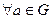
3) 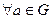 существует симметричный (обратный)
существует симметричный (обратный) 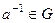 , т.е.
, т.е. 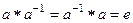 .
.
Примеры.
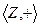 ,
, 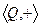 ,
, 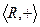 - «аддитивные» группы (по сложению).
- «аддитивные» группы (по сложению).
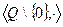 ,
, 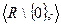 - «мультипликативные» группы (по умножению).
- «мультипликативные» группы (по умножению).
Если операция коммутативна, то группа называется коммутативной, или абелевой.
Дата добавления: 2020-11-18; просмотров: 814;











