БИНАРНЫЕ ОТНОШЕНИЯ. Основные определения
Определение 1.1. Пусть A – некоторое множество. Рассмотрим декартово произведение 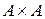 и некоторое его подмножество
и некоторое его подмножество 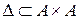 . Тогда
. Тогда 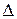 называется бинарным отношением на множестве A.
называется бинарным отношением на множестве A.
Говорят, что элемент 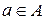 находится в отношении
находится в отношении 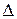 с элементом
с элементом 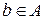 , если упорядоченная пара
, если упорядоченная пара 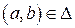 . Этот факт также записывают в виде
. Этот факт также записывают в виде 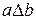 .
.
Примеры. 1) Пусть 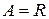 . Определим бинарное отношение
. Определим бинарное отношение 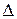 на множестве R следующим образом:
на множестве R следующим образом: 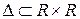 ,
, 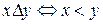 .
.
2) Пусть A – множество студентов потока, тогда 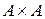 – множество упорядоченных пар студентов. Рассмотрим
– множество упорядоченных пар студентов. Рассмотрим 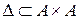 , определяемое следующим образом:
, определяемое следующим образом: 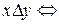 студенты x и y учатся в одной группе.
студенты x и y учатся в одной группе.
Рассмотрим ряд определений, связанных с понятием бинарного отношения.
Определение 1.2. Пусть 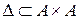 ,
, 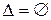 , т. е. отношение
, т. е. отношение 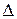 не выполняется ни для одной пары элементов множества A. Тогда отношение
не выполняется ни для одной пары элементов множества A. Тогда отношение 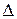 называется пустым .
называется пустым .
Пример. Пусть 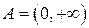 , тогда
, тогда 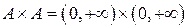 . Рассмотрим отношение
. Рассмотрим отношение 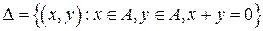 . Очевидно, что
. Очевидно, что 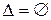 .
.
Определение 1.3. Пусть 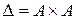 . Тогда отношение
. Тогда отношение 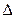 называется полным.
называется полным.
Определение 1.4. Пусть 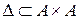 . Рассмотрим бинарное отношение
. Рассмотрим бинарное отношение 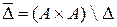 . Бинарное отношение
. Бинарное отношение 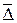 называется дополнительным к бинарному отношению
называется дополнительным к бинарному отношению 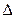 .
.
Пример. Рассмотрим предыдущий пример, где A – множество студентов потока и бинарное отношение 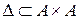 определяется так:
определяется так: 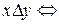 студенты x и y учатся в одной группе. Тогда
студенты x и y учатся в одной группе. Тогда 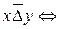 студенты x и y учатся в разных группах.
студенты x и y учатся в разных группах.
Определение 1.5. Пусть 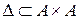 . Рассмотрим бинарное отношение
. Рассмотрим бинарное отношение 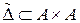 , определяемое следующим образом:
, определяемое следующим образом: 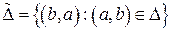 . Бинарное отношение
. Бинарное отношение 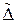 называется противоположным бинарному отношению
называется противоположным бинарному отношению 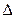 .
.
Примеры. 1) Пусть 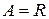 . Пусть
. Пусть 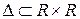 ,
, 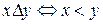 . Тогда
. Тогда 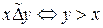 .
.
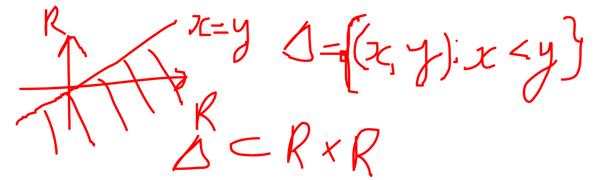
2) Пусть A – множество студентов потока и бинарное отношение 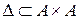 определяется так:
определяется так: 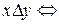 студенты x и y учатся в одной группе. Тогда, очевидно,
студенты x и y учатся в одной группе. Тогда, очевидно, 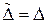 .
.
Дата добавления: 2021-02-19; просмотров: 616;











