Основы молекулярной физики и термодинамики

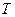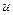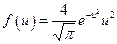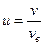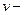Задача 1.Двухатомный идеальный газ с молярной массой М находится при температуре . Используя функцию распределения молекул идеального газапо относительным скоростям : , где , скорость теплового движения молекул, 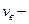наиболее вероятная скорость молекул, определите (в процентах) вероятность того, что молекулы идеального газа имеют скорости теплового движения в интервале от 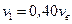до .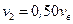

Дано: , , .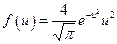

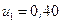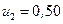Определить: .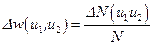

Решение. Число 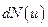молекул, относительные скорости которых находятся в пределах от 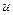до 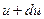, определяется выражением ,

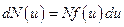где 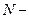число молекул в объеме газа, 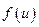– функция распределения, 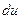–заданный малый интервал скоростей. Искомая вероятность будет равна .

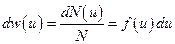Учитывая малость интервала относительных скоростей, можно считать, что мы ищем величину 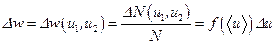, где 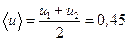, , 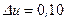поэтому 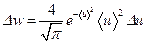. Подставляя числовые значения исходных величин, получим ; .

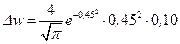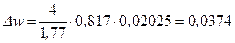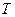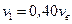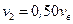Ответ: При заданных значениях М и вероятность обнаружить молекулы идеального газа со скоростями, находящимися в интервале от до равна .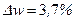

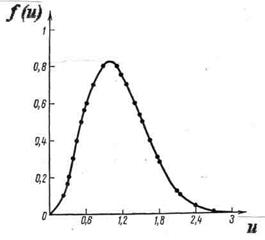
Примечание. Таким же методом можно определить вероятность того, что молекулы идеального газа имеют скорости теплового движения в любом конечном интервале относительных скоростей от до 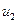. Для этого необходимо разбить этот интервал 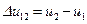на некоторое число 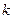интервалов 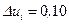, т.е. принять, что 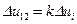и провести вычисления вышеизложенным методом, т.е. найти вероятности 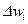. Искомая вероятность .

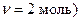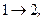
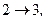
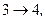
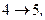
Задача 2. Идеальный двухатомный газ (молекулы с жесткой связью, находится в состоянии 1, параметры которого показаны на графике (см. рис.). Путем последовательного применения изопроцессов: 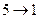газ переводится в исходное состояние (совершает цикл – круговой замкнутый процесс). Укажите, как называется каждый из этих изопроцессов. Для каждого из указанных процессов определите:

изменение внутренней энергии 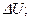совершенную работу 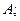переданное количество теплоты 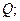изменение энтропии 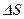; а так же работу, совершенную газом за весь цикл, и КПД цикла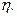

Дано: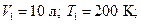

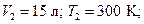
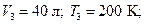
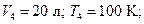
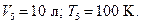
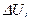
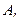
Определить: 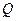и 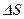(для каждого процесса); и

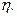
Решение.

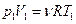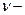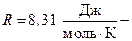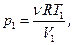
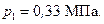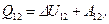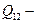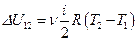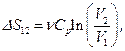1)Процесс – изобарный, из уравнения Менделеева – Клапейрона , где количество вещества, молярная газовая постоянная, находим На основании первого закона термодинамики: где количество теплоты полученное газом, – изменение внутренней энергии газа, – работа газа при изобарном расширении.Изменение энтропии газа в изобарном процессе определяется выражением: где 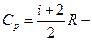изобарная теплоемкость газа, – число степеней свободы (двухатомный газ). Подставив числовые значения, найдем:

,

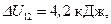
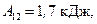
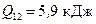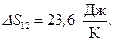
2) Процесс 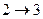– адиабатный, поэтому 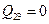и 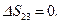Работа расширения газа в адиабатном процесс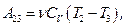е где 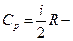изохорная теплоемкость газа, а изменение внутренней энергии газа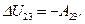

Подставив числовые значения, найдем:

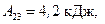
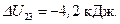
4) Процесс 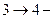изобарный.

3) Процесс 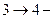изобарный. Из уравнения Менделеева – Клапейрона 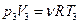, находим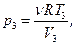 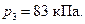Аналогично пункту [1] определим в этом процессе изменение внутренней энергии 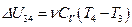, работу газа 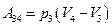и изменение энтропии 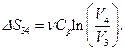Подставив числовые значения, найдем:

,

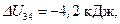
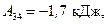
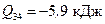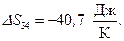
4) Процесс 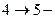изотермический, поэтому изменение внутренней энергии в этом процессе 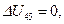количество теплоты и работа 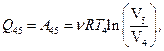а изменение энтропии

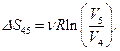Подставив числовые значения, найдем: ,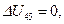

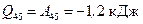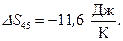
5) Процесс 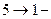изохорный, поэтому работа газа 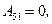количество теплоты и изменение внутренней энергии 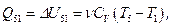а изменение энтропии 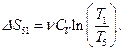Подставив числовые значения, найдем: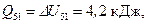

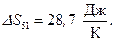
Работа цикла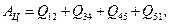

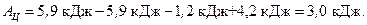
КПД цикла 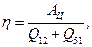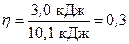или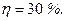

Подставив числовые значения, можно убедиться, что для всего цикла 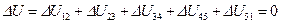и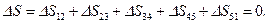

Задача 3. Найти среднюю кинетическую энергию 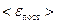поступательного движения одной молекулы кислорода при температуре 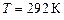, а также кинетическую энергию 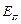поступательного движения всех молекул, содержащих кислорода.

Решение. Средняя кинетическая энергия поступательного движения одной молекулы любого газа равна

,

где 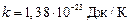– постоянная Больцмана. Подставляя в значения k и температуры, находим

.

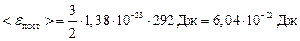Кинетическую энергию поступательного движения всех молекул найдём, если умножим среднюю энергию 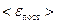одной молекулы на число N молекул, которое можно определить из соотношения

,

где 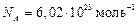– число Авогадро, – молярная масса кислорода. Таким образом,

,

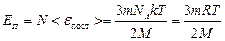где 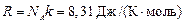– универсальная газовая постоянная. Подставляя в числовые значения, находим

.

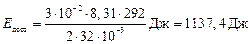Ответ: ; .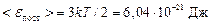

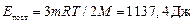Задача 4. Вычислить удельные теплоёмкости при постоянном объёме 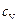и при постоянном давлении 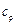неона и водорода, принимая эти газы за идеальные.

Решение. Удельные теплоёмкости идеальных газов выражаются формулами:

, ,

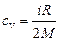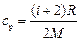где i – число степеней свободы молекулы газа;

M – молярная масса.

Для неона (одноатомный газ) 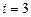и молярная масса .

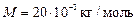Произведём вычисления:

,

.

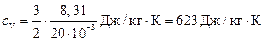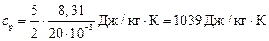Для водорода (двухатомный газ) и молярная масса 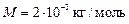. Тогда

,

.

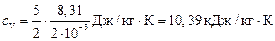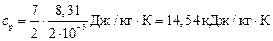Ответ: Для неона , ;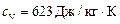

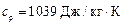для водорода , .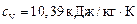

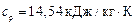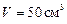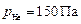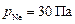Задача 5. Разрядная трубка гелий-неонового лазера объёмом заполняется смесью гелия и неона с парциальными давлениями и , соответственно. Определить внутреннюю энергию газов.

Решение. Внутреннюю энергию идеального газа можно определить из соотношения

,

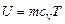где 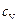– удельная теплоёмкость газа при постоянном объёме, T – температура газа, m – масса газа. Так как внутренняя энергия является аддитивной величиной, то для смеси газов она равна

,

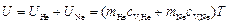где 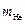, 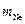– массы гелия и неона, 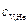, 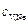– их удельные теплоёмкости.

Для удельной теплоёмкости идеального газа имеем формулу

,

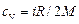где 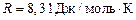– молярная газовая постоянная, i – число степеней свободы молекулы газа. Так как газы гелий и неон являются одноатомными, то для них 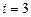. Поэтому их удельные теплоёмкости равны

,

.

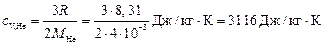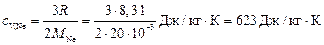Подставляя выражение в выражение для внутренней энергии , находим

,

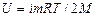откуда

, .

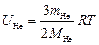Парциальные давления каждого газа в смеси газов удовлетворяют уравнению Клапейрона-Менделеева, т.е.

, .

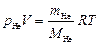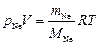Подставляя правые части уравнений в уравнения , получаем

, .

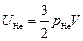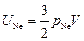Произведём вычисления:

, .

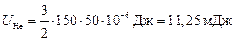Внутренняя энергия смеси газов равна

.

Ответ: ; ; .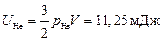

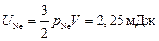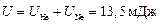Задача 6. Двухатомный газ занимает объём 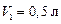и находится под давлением 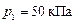. Газ сжимается адиабатически до некоторого объёма 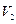и давления 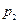. Затем он охлаждается при 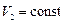до первоначальной температуры, причём его давление становится равным 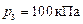. Построить график этого процесса. Найти объём 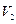и давление .

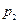Решение. Исходя из данных условия задачи, построим график процесса, который изображён на рисунке.

Запишем уравнение Клапейрона-Менделеева для газа в состояниях 1, 2 и 3:

, , ,

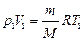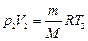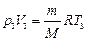где m – масса газа;

M – молярная масса газа.

По условию задачи состояния 1 и 2 связаны соотношением

,

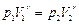а для состояний 2 и 3 имеют место условия

, , .

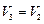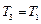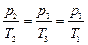Постоянная адиабаты определяется как

,

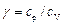где 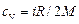– удельная теплоёмкость газа при постоянном объёме;

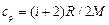– удельная теплоёмкость газа при постоянном давлении;

i – число степеней свободы молекулы газа.

Молекула двухатомного газа имеет 5 степеней свободы, . Следовательно, постоянная адиабаты для такого газа равна

.

Так как в уравнениях 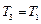и 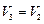, то левые части первого и третьего уравнений равны, т.е.

,

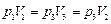откуда находим объём :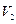

.

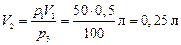Давление 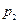найдём из уравнения адиабаты

.

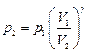Произведём вычисления:

.

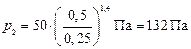Ответ: 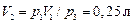; 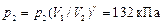, где для двухатомного газа .

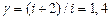Задача 7. Газ, совершая цикл Карно, к.п.д. которого 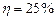, при изотермическом расширении производит работу 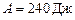. Какова работа, совершаемая газом при изотермическом сжатии?

Решение. КПД цикла Карно определяется по формуле

,

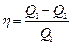где 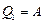– теплота, полученная от теплоотдатчика, равная работе, совершаемой газом при расширении, 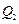– количество тепла, отданное газом холодильнику, равное работе, совершаемой над газом при его сжатии. Поэтому работа газа при его сжатии будет отрицательной и равной 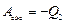. Таким образом, из получаем

.

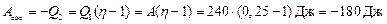Ответ: .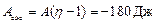

Электродинамика

Пример 1 Два точечных заряда 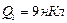и 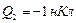закреплены на расстоянии 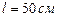друг от друга. Третий заряд Q₃ может перемещаться только вдоль прямой, проходящей через заряды. Определить положение заряда Q₃, при котором он будет находиться в равновесии. При каком знаке заряда Q₃ равновесие будет устойчивым?

Решение. Заряд Q₃ будет находиться в равновесии в том случае, если геометрическая сумма сил, действующих на него, равна нулю. Поскольку на заряд Q₃ будут действовать только кулоновские силы F₃₁ и F₃₂ со стороны зарядов Q₁ и Q₂, соответственно, то равновесие будет иметь место, если эти силы уравновешивают друг друга.

Выберем в качестве начала отсчёта точку, в которой находится заряд Q₁. Обозначим расстояние между зарядом Q₁ и Q₃ через x. Тогда возможны три случая расположения заряда Q₃ по отношению к зарядам Q₁ и Q₂, которые показаны на рисунке 3.8 (заряд Q₃ показан положительным; если заряд Q₃ отрицателен, направления сил изменятся на противоположные).

В случае а) на заряд Q₃ действуют противоположно направленные силы F₃₁ и F₃₂, равные по величине

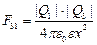и ,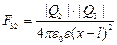

соответственно. Так как 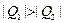, и число с большим знаменателем меньше числа с меньшим знаменателем, то получаем следующую цепочку неравенств:

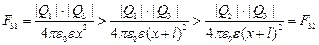
то есть величина силы F₃₁ всегда больше величины силы F₃₂ , что означает, что в случае а) равновесие невозможно.

В случае б) силы F₃₁ и F₃₂, действующие на заряд Q₃, направлены в одну сторону. Следовательно, и в этом случае равновесие невозможно.

В случае в) на заряд Q₃ действуют противоположно направленные силы F₃₁ и F₃₂, равные по величине

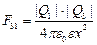и ,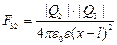

соответственно. Приравнивая эти силы, получаем уравнение для определения x:

,

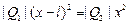откуда следуют два решения:

;

.

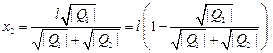Очевидно, второе решение x₂ не удовлетворяет физическому условию, так как 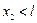. Таким образом, остаётся первое решение, причём величина заряда Q₃ не играет роли:

.

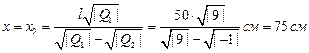Определим теперь знак заряда Q₃, при котором равновесие будет устойчивым. Равновесие будет устойчивым, если при смещении заряда Q₃ от положения равновесия, на него начнёт действовать результирующая сила, которая стремится возвратить его в положение равновесия.

Пусть заряд Q₃ положителен. Смещая его вправо на Dx, получаем следующее соотношение между силами

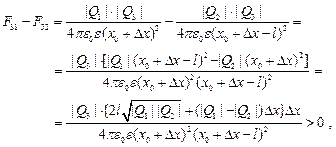
то есть сила F₃₂, которая направлена в сторону положения равновесия, по величине меньше силы F₃₁. При смещении этого заряда влево, т.е. при 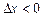, будем иметь

,

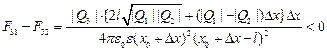то есть сила F₃₂, которая направлена от положения равновесия, по величине меньше силы F₃₁, направленной в сторону положения равновесия. Следовательно, при смещении от положения равновесия вправо или влево положительный заряд Q₃ будет удаляться от него и равновесие будет неустойчивым.

Пусть теперь заряд Q₃ отрицателен. Аналогично смещая его вправо или влево на Dx, получаем соотношения (1) и (2) между силами, действующими на заряд, но их направления будут противоположными Соотношения (1) и (2) будут теперь означать, что отрицательный заряд стремится вернуться в положение равновесия. Следовательно, положение равновесия будет устойчивым только для отрицательного заряда.

Чтобы определить величину заряда Q₃, рассмотрим силы, действующие, например, на заряд Q₂. Если на заряд Q₂ не действуют другие силы, кроме электростатических, то равновесие заряда Q₂ означает равенство сил

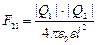и ,

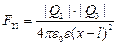действующих со стороны зарядов Q₁ и Q₃, соответственно. Из равенства этих сил следует

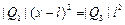
откуда получаем

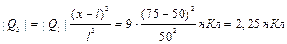
Если равновесие зарядов Q₁ и Q₂ поддерживается механическими силами, то равновесие заряда Q₃ будет иметь место при любой его величине.

Ответ: 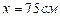от положительного заряда и 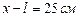от отрицательного заряда; если заряды Q₁ и Q₂ закреплены жёстко, то величина заряда Q₃ несущественна; в противном случае при устойчивом равновесии .

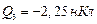Пример 2 Три точечных заряда 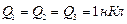Расположены в вершинах равностороннего треугольника. Какой заряд Q₄ нужно поместить в центре треугольника, чтобы указанная система зарядов находилась в равновесии?

Решение. Все три заряда, расположенные по вершинам треугольника, находятся в одинаковых условиях. Поэтому достаточно выяснить, какой заряд следует поместить в центре треугольника, чтобы какой-нибудь один из трёх зарядов, например Q₁, находился в равновесии. Заряд Q₁ будет находиться в равновесии, если векторная сумма действующих на него сил равна нулю (рисунок 3.9):

,

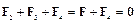где F₁, F₂, F₃ – силы, с которыми действуют на заряд Q₁ заряды Q₂, Q₃, Q₄, соотвественно;

F – равнодействующая сил F₂ и F₃.

Так как силы F и F₄ направлены по одной прямой в противоположные стороны, то векторное равенство можно заменить скалярным:

.

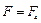Выразив F через F₂ и F₃ и учитывая, что 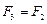, получим

.

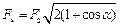Применив закон Кулона, и имея в виду, что 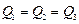, найдём

,

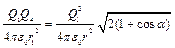откуда

.

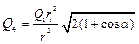Из геометрических построений в равностороннем треугольнике следует, что

.

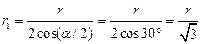С учётом этого из формулы получим

.

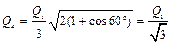Производя вычисления, находим

.

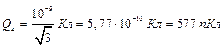Следует отметить, что равновесие системы зарядов будет неустойчивым.

Ответ: .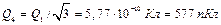

Пример 3 На тонком стержне длиной 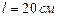находится равномерно распределённый электрический заряд. На продолжении оси стержня на расстоянии 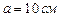от ближайшего конца находится точечный заряд 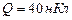, который взаимодействует со стержнем с силой 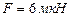. Определить линейную плотность t заряда на стержне.

Решение. Сила взаимодействия F заряженного стержня с точечным зарядом Q зависит от линейной плотности t заряда на стержне. Зная эту зависимость, можно определить t. При вычислении силы F следует иметь в виду, что заряд на стержне не является точечным, поэтому закон Кулона непосредственно применить нельзя. В этом случае можно поступить следующим образом. Выделим в стержне малый участок dr с зарядом 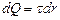(рисунок 3.10). Этот заряд можно рассматривать как точечный. Тогда согласно закону Кулона

.

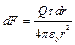Интегрируя это выражение в пределах от a до l+a, получаем

,

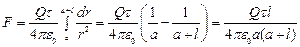откуда

.

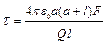Произведём вычисления:

.

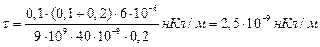Ответ: .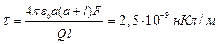

Пример 4 Два точечных электрических заряда 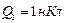и находятся в воздухе на расстоянии 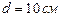друг от друга. Определить напряжённость E и потенциал j поля, создаваемого этими зарядами в точке A, удалённой от заряда Q₁ на расстояние 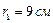и от заряда Q₂ на расстояние .

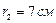Решение. Результирующее электрическое поле двух зарядов в точке можно определить исходя из принципа суперпозиции полей, согласно которому поле каждого заряда не зависит от присутствия других зарядов. Поэтому напряжённость электрического поля E в точке A равна векторной, или геометрической сумме напряжённостей E₁ и E₂ электрических полей, создаваемых каждым зарядом в отдельности: 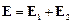(см. рисунок 3.11). Величины напряжённостей электрического поля зарядов Q₁ и Q₂ в воздухе (e = 1) в точке A равны:

, .

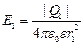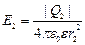Так как заряд Q₁ положителен, то вектор E₁ направлен вдоль силовой линии поля от заряда, тогда как вектор E₂ направлен вдоль силовой линии поля к отрицательному заряду Q₂. Величину вектора E можно найти по теореме косинусов:

,

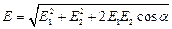где a – угол между векторами E₁ и E₂. Из теоремы косинусов для треугольника Q₁AQ₂ следует:

,

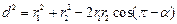откуда

.

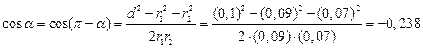Следовательно, величина суммарной напряжённости поля равна

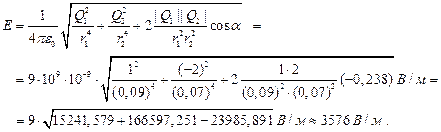
В соответствии с принципом суперпозиции потенциал результирующего поля, создаваемого двумя зарядами Q₁ и Q₂, равен алгебраической сумме потенциалов: j = j₁ + j₂. Потенциалы зарядов Q₁ и Q₂ в точке A равны

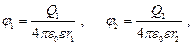
так что результирующий потенциал равен

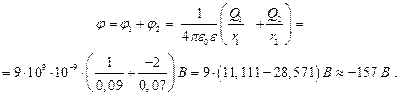
Ответ: ; .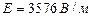

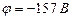Пример 5 Точечный заряд 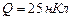находится в поле, созданном прямым бесконечным цилиндром радиуса 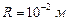, равномерно заряженным с поверхностной плотностью 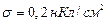. Определить силу F, действующую на заряд, если его расстояние от оси цилиндра .

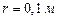Решение. Значение силы F, действующей на точечный заряд Q, находящийся в электрическом поле, определяется по формуле

,

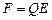где E – напряжённость поля.

Напряжённость поля бесконечно длинного равномерно заряженного цилиндра можно найти, используя теорему Гаусса. Для этого окружим цилиндр коаксиальной цилиндрической поверхностью радиусом r и высотой h и замкнём её двумя основаниями S₁ и S₂ (рисунок 3.12). После этого рассчитаем поток вектора напряжённости электрического поля. Он может быть представлен как сумма потоков через два основания S₁ и S₂ и через боковую поверхность S_бок. По теореме Гаусса имеем

,

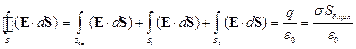где 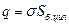– заряд, сосредоточенный на боковой поверхности 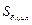части цилиндра, находящейся внутри замкнутой поверхности.

В силу симметрии задачи напряжённость поля E во всех точках боковой поверхности S_бок имеет одинаковую величину и направлена перпендикулярно оси цилиндра в сторону от неё. Иначе говоря, напряжённость поля E всегда параллельна нормали к элементу площади боковой поверхности. С другой стороны, она перпендикулярна нормалям к элементам поверхностей оснований S₁ и S₂, как это показано на рисунке 3.12. Следовательно, потоки вектора E через основания S₁ и S₂ равны нулю. Поток же через боковую поверхность равен

.

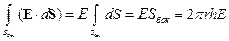Боковая поверхность части цилиндра, находящейся внутри замкнутой поверхности, равна

.

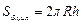Подставляя формулы и в , получаем выражение для величины напряжённости электрического поля вне цилиндра на расстоянии 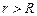от оси цилиндра:

.

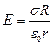Наконец, подставив в , получим силу

.

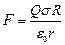Произведём вычисления:

.

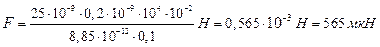Ответ: .

Пример 6 . По тонкой нити, изогнутой по дуге окружности, равномерно распределён заряд с линейной плотностью 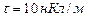. Определить напряжённость E и потенциал j электрического поля, создаваемого таким распределённым зарядом в точке, совпадающей с центром кривизны дуги. Длина нити составляет одну треть длины окружности и равна .

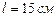Решение. Выберем оси координат так, чтобы начало координат совпадало с центром кривизны дуги, а ось Y была бы симметрично расположена относительно концов дуги (рисунок 3.13). На нити выделим элемент длины dl. Заряд 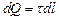, находящийся на выделенном участке, можно считать точечным.

Определим напряжённость электрического поля в начале координат. Для этого найдём сначала напряжённость dE поля, создаваемого зарядом dQ:

,

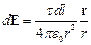где r – радиус-вектор, направленный от элемента dl к точке, в которой напряжённость поля вычисляется.

Выразим вектор dE через проекции dE_x и dE_y на оси координат:

,

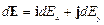где i и j – единичные векторы направлений (орты).

Напряжённость E найдём посредством интегрирования:

.

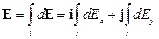Интегрирование ведётся вдоль дуги длиной l.

В силу симметрии

.

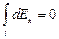Тогда

,

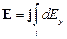где .

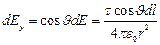Так как 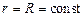, , 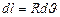то

.

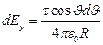Подставим это выражение dE_y в и, приняв во внимание симметричное расположение дуги относительно оси Y, пределы интегрирования возьмём от 0 до p/3, а результат удвоим:

.

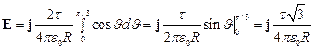Выразив радиус R через длину l нити ( 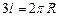), получим

.

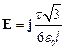Из этой формулы видно, что напряжённость поля по направлению совпадает с осью Y.

Найдём потенциал электрического поля в начале координат. Сначала запишем потенциал, создаваемый точечным зарядом dQ в этой точке:

.

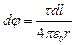Заменим r на R и проведём интегрирование:

.

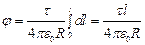Так как 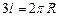, то

.

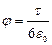Произведём вычисления по формулам и :

,

.

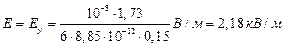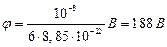Ответ: ; .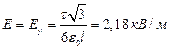

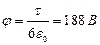Пример 7 На пластинах плоского воздушного конденсатора находится заряд 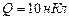. Площадь каждой пластины конденсатора равна 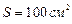. Определить силу F, с которой притягиваются пластины. Поле между пластинами считать однородным.

Решение. Заряд Q одной пластины находится в поле напряжённости E, созданном зарядом другой пластины конденсатора. Следовательно, на этот заряд действует сила

.

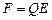Так как поле однородно, то можно считать, что оно создаётся плоской бесконечной пластиной. Напряжённость такого поля определяется по формуле

,

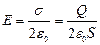где s – поверхностная плотность заряда пластины.

Формула примет вид

.

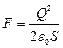Произведём вычисления:

.

Ответ: .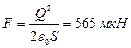

Пример 8 Электрическое поле создано длинным цилиндром радиусом 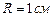, равномерно заряженным с линейной плотностью 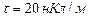. определить разность потенциалов между двумя точками этого поля, находящихся на расстояни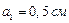и и 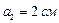от поверхности цилиндра в средней его части.

Решение. Для определения разности потенциалов воспользуемся соотношением между напряжённостью поля и изменением потенциала: 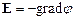. Для поля с осевой симметрией, каким является поле цилиндра, это соотношение можно записать в виде

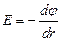, или .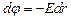

Интегрируя это выражение, найдём разность потенциалов между двумя точками, отстоящими на расстояниях r₁ и r₂ от оси цилиндра:

.

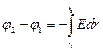Так как цилиндр длинный и