Абсолютно упругий удар
Это такой удар, при котором не происходит необратимых преобразований кинетической энергии во внутреннюю энергию тел.
При абсолютно упругом ударе свободных тел сохраняется кинетическая энергия системы и ее импульс. Формы всех тел после завершения удара восстанавливаются.
Упругое столкновение в макроскопическом мире — это недостижимый идеальный случай, так как часть кинетической энергии тел всегда переходит в другие виды энергии (тепловую, звуковую и т. п.).
Абсолютно неупругий удар
Это удар, при котором после столкновения тела «слипаются».
При абсолютно неупругом соударении свободных тел импульс системы сохраняется, а ее кинетическая энергия уменьшается (потерянная кинетическая энергия переходит во внутреннюю энергию — тела нагреваются). Деформации тел в процессе такого удара постоянно нарастают и формы тел после завершения удара не восстанавливаются .
Реальные удары
Абсолютно упругий и абсолютно неупругий удары — это идеальные предельные случаи. При соударении реальных тел имеют место элементы, свойственные как упругим, так и неупругим ударам.
Характерные свойства абсолютно упругого и абсолютно неупругого ударов наглядно проявляются в системе отсчета, связанной с центром масс сталкивающихся тел. В этой системе отсчета удары выглядят очень просто.
| Абсолютно упругий удар | Абсолютно неупругий удар | Удар реальных тел |
Тела движутся навстречу друг другу со скоростями vv v2 и после удара расходятся с такими же скоростями:
v 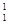 = v1, v = v1, v 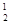 =v2 =v2
| Тела движутся навстречу друг другу со скоростями v1, v2 и после удара останавливаются:
v 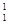 =0, v =0, v 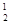 =0 =0
| Тела движутся навстречу друг другу со скоростями v1, v2 и после удара расходятся со скоростями:
v 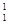 =kv1, v =kv1, v 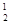 = kv2
(0 < k< 1). = kv2
(0 < k< 1).
|
| Таким образом, в системе центра масс величины скоростей не изменяются | Таким образом, в системе центра масс величины скоростей после удара становятся равными нулю | Таким образом, в системе центра масс величины скоростей изменяются одинаково |
Коэффициент k одинаков для обоих тел и показывает в системе центра масс, чему равно отношение величины скорости тела после удара (v1) к величине скорости до удара:

Его называют коэффициентом восстановления скорости. Он характеризует степень упругости. Если k = 1, то удар абсолютно упругий (удар стального шара о стальную плиту); если k = О, то удар абсолютно неупругий (удар комка влажной глины о плиту).
При игре в теннис коэффициент восстановления может принимать значения до 0,7.
Игра в теннис
При игре в теннис резкое изменение характера движения мяча при ударе ракетки обусловлено силой, действующей на него со стороны ракетки. Время действия силы удара очень мало, но ее величина весьма значительна. И мяч, и ракетка при столкновении деформируются довольно сильно (рис. 9.13).
Подача мяча при игре в теннис — пример неупругого соударения. Все параметры удара представлены на рис. 9.14.
Ракетка массой М со скоростью v0 ударяет по неподвижному мячу массой т. После того, как мяч отделился от поверхности ракетки, он движется со скоростью и, а скорость ракетки после этого становится v. Рассматривая ракетку и мяч как изолированную систему, можно записать закон сохранения импульса:
Mv0 =Mv + ти.
Высокоскоростная съемка позволяет определить скорость ракетки в момент удара и после удара, а также скорость мяча после удара. Найденные таким путем скорости можно использовать для вычисления потерь кинетической энергии при выполнении подачи. Для профессионального игрока разность между кинетической энергией ракетки перед ударом и суммарной кинетической энергией ракетки и мяча после удара составляет приблизительно 30—35 Дж. Эта энергия превращается в другие формы энергии, а именно в тепловую и звуковую ( всегда слышен удар ракетки по мячу).

Рис. 9.13.Удар теннисной ракеткой по мячу: деформируются оба тела

Рис. 9.14.Взаимодействие ракетки и мяча при игре в теннис
Удар ногой по мячу
При изучении баллистического движения спортсменов, выполняющих удары, было обнаружено, что, если в начале выполнения такого движения все усилия, приложенные к центрам тяжести звеньев кинематической цепи (нога), направлены по ходу движения, то перед самым соприкосновением с ударяемым предметом эти усилия меняют свое направление на обратное (рис. 9.15).
Физиологически этому торможению соответствует активность антагонистов (совершенно пассивных в начальной фазе движения), хорошо прослеживаемая при отведении биоэлектрических потенциалов соответствующих мышц ( рис. 9.16).
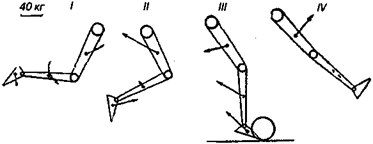
Рис. 9.15.Направление усилий, приложенных к центрам тяжести звеньев ноги
спортсмена, выполняющего удар по мячу: / и // — начало движения; ///— момент соприкосновения стопы с мячом; IV— момент после удара

Рис. 9.16.Биоэлектрическая активность мышц ноги спортсмена,
выполняющего удар по мячу: 1 — прямая мышца бедра; 2 — двуглавая мышца бедра; 3 — передняя большеберцовая ; 4 — икроножная
Описываемое явление имеет под собой совершенно определенные физические причины. При нанесении любого удара весьма важно превратить мягкую кинематическую цепь ноги в единый жесткий рычаг (сделать ее стержнем). В этом случае в ударе примет участие не только масса конечного звена цепи, но и массы всех остальных звеньев (что заметно повышает массу ударяющего предмета). Превратившись в жесткую систему, кинематическая цепь конечности не будет в самые решающие мгновения амортизировать и, следовательно, передаст ударяемому предмету максимально возможное количество кинетической энергии.
Дата добавления: 2020-11-18; просмотров: 1198;











