Скорость звука в газах
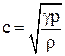 ,
,
где p – давление газа, не возмущенного волной;
r – плотность газа, не возмущенного волной;
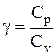 – отношение молярной теплоемкости газа при постоянном давлении к теплоемкости газа при постоянном объеме.
– отношение молярной теплоемкости газа при постоянном давлении к теплоемкости газа при постоянном объеме.
Амплитуда звукового давления Dp0 и амплитуда скорости v0 частиц в звуковой волне связаны соотношением
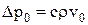 .
.
Интенсивность звука I, выраженная через амплитуду звукового давления – энергия, переносимая звуковой волной за единицу времени через единичную площадку, перпендикулярную направлению распространения волны:
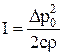 ,
,
где r – плотность газа.
Уровень интенсивности звука (в децибелах) определяется формулой
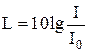 ,
,
где I – интенсивность данного звука;
I0 = 10–12 Вт/м2 – интенсивность звука на пороге слышимости при стандартной частоте n = 1 кГц.
Уровень громкости звука (в фонах) вычисляется по формуле
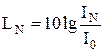 ,
,
где IN – интенсивность звука стандартной частоты n = 1 кГц, равногромкого с исследуемым звуком.
Явление Доплера – если источник и приемник звука перемещаются относительно среды, в которой распространяется звук, то частота звуковых колебаний n', регистрируемая приемником звука, связана с частотой собственных колебаний n источника соотношением
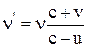 ,
,
где c, u, v – скорости соответственно звука, его источника и приемника.
Примечание. Записанная формула относится к случаю, если источник и приемник звука движутся по одной прямой. При этом величины u, v – алгебраические: u > 0, если источник движется к приемнику; u < 0, если источник удаляется от приемника. Аналогично v > 0, если приемник приближается к источнику; v < 0, если приемник движется от источника.
Вектор плотности потока энергии волны – физическая величина, модуль которой равен энергии DW, переносимой волной за единицу времени (Dt = 1) через единичную площадку, расположенную перпендикулярно направлению распространения волны (DS^):
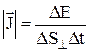 ;
; 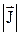 = u v; J = u×v,
= u v; J = u×v,
где u – плотность энергии в каждой точке среды, среднее значение которой вычисляется по формуле 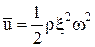 ;
;
ρ – плотность среды;
x0 – амплитуда волны;
w – круговая (циклическая частота);
v – фазовая скорость (скорость перемещения фазы волны).
Энергия, работа, мощность. Законы
сохранения в механике
Энергия – количественная мера и качественная характеристика движения и взаимодействия материи во всех ее превращениях. Она является функцией состояния системы и характеризует способности системы к совершению работы при переходе из одного состояния в другое.
Изменение энергии при переходе системы из одного состояния в другое равно работе, совершаемой системой в процессе перехода:
DW = W1 – W2 = A.
Диссипация (рассеяние) энергии механических систем –процесс перехода части их механической энергии в другие формы под влиянием внешних факторов (например, за счет наличия сил сопротивления).
Диссипативные системы – системы, в которых полная механическая энергия постепенно уменьшается за счет преобразования в другие (немеханические) формы, например в теплоту.
Механическая энергия – физическая величина, равная работе, которая может быть произведена при полном превращении движения данной формы в механическую форму движения материи.
Кинетическая энергия - физическая величина, характеризующая способность движущегося тела или системы совершать работу при торможении до полной остановки – одна из функций состояния ее движения:
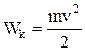 .
.
Кинетическая энергия системы – сумма кинетических энергий отдельных тел (материальных точек) этой системы:
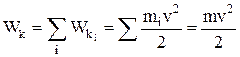 ,
,
где 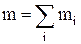 – масса тела (системы);
– масса тела (системы);
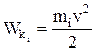 – кинетическая энергия i-го тела системы.
– кинетическая энергия i-го тела системы.
Связь между кинетической энергией тела (системы) и его импульсом:
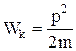 .
.
Кинетическая энергия при вращательном движении:
1) элементарной массы Dmi:
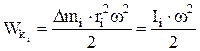 ,
,
где Ii = Dmi∙ri2 – момент инерции материальной точки, относительно выбранной оси вращения;
2) тела (системы):
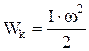 ,
,
где 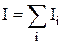 – момент инерции тела относительно той же оси вращения.
– момент инерции тела относительно той же оси вращения.
Потенциальная энергия–физическая величина, характеризующая способность системы совершать работу, связанную с изменением конфигурации и взаимного расположения тел или частей в системе.
Изменение потенциальной энергии системы зависит только от начального и конечного ее состояний и равно работе внутренних (консервативных) сил системы, взятой с обратным знаком:
dWp = –dA.
Характеристики поля тяготения – напряженность и потенциал поля тяготения.
Напряженностью поля тяготения в данной точке называется векторная физическая величина, равная по величине и направлению силе, действующей на единичную массу, помещенную в данную точку поля:
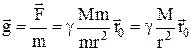 .
.
Потенциалом поля тяготения называют скалярную физическую величину, равную потенциальной энергии единичной массы, помещенной в данную точку поля:
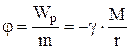 ,
,
т.е. потенциал поля тяготения тоже с увеличением расстояния увеличивается и при r ® ¥ равен нулю.
Связь между напряженностью и потенциалом поля тяготения:
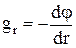 .
.
Дата добавления: 2022-02-05; просмотров: 542;











