Период колебаний крутильного маятника

,

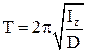где I_z – момент инерции тела относительно оси колебаний.

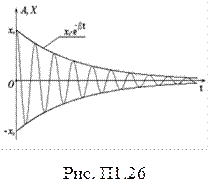
Затухающие (свободные) колебания –движения реальной колебательной системы, сопровождающиеся силами трения и сопротивления, которые приводят к уменьшению амплитуды колебаний (рис. П1.26). При этом энергия, потерянная системой, не восполняется за счет внешних сил.

Дифференциальное уравнение затухающих колебаний:

,

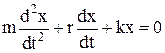где r – коэффициент сопротивления.

Решение уравнения затухающих колебаний:

,

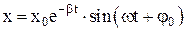где А = x₀ e^{– βt} – амплитуда колебаний, убывающая по экспоненциальному закону;

β = r/(2m) – коэффициент затухания, характеризующий быстроту убывания амплитуды с течением времени;

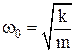– собственная частота колебаний системы, т.е. та частота, с которой совершались бы свободные колебания системы в отсутствии сопротивления среды (r = 0).

Круговая частота, частота и период затухающих колебаний:

; ; .

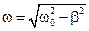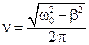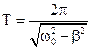Характеристики затухающих колебаний:

1) декремент затухания – отношение двух смещений, отличающихся друг от друга по времени на период. Декремент затухания характеризует быстроту затухания в зависимости от числа колебаний:

;

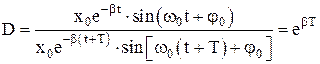2) логарифмический декремент затухания –величина, равная натуральному логарифму от декремента затухания. Логарифмический декремент затухания характеризует затухание колебаний за период:

l = lnD = ln(e^βΤ) = βT.