Справочная информация

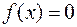Как известно, далеко не всякое алгебраическое уравнение может быть решено аналитически. Это относится к большинству трансцендентных уравнений и к алгебраическим уравнениям выше четвёртого порядка. Однако точное решение уравнений на практике часто и не требуется. Чтобы считать задачу решённой, достаточно бывает отыскать значения корней с требуемой степенью точности. Для получения таких решений разработаны численные методы.

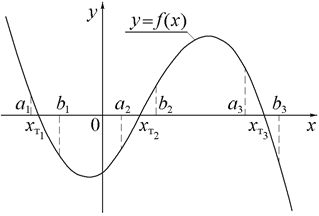
Решение нелинейных уравнений осу­­­ществляется в два этапа. На первом этапе производится отделение корней, то есть поиск достаточно малых отрезков локализации, каждый из которых содержит единственный корень уравнения и на каждом из которых функция f(x) монотонна вместе со своей первой производной. Для этого используется график функции y = f(x), точки пересечения которого с осью абсцисс являются корнями исходного уравнения.

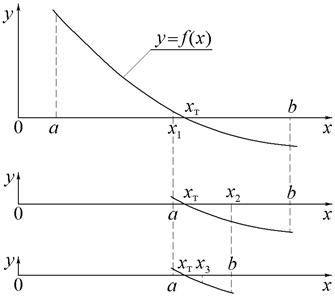
Случай, когда корнем уравнения является точка касания графика и оси абсцисс, здесь не рассматривается. Это позволяет выделить отрезки [a, b], содержащие только один корень (см. рис.1). При этом для непрерывной функции f(x) будет выполняться неравенство f(a) f(b) < 0.

Процесс отделения корней может быть проиллюстрирован на примере уравнения x³– 7.3x²+16.8x – 12.2 = 0, для которого корни ищутся на отрезке [0, 3]. Сначала выполняется процесс табулирования функции f(x)= x³– 7.3x²+16.8x – 12.2 , а затем, используя полученные результаты, строится диаграмма типа «гладкие графики» (см. рис.2). Как видно из графика функции, на этом этапе можно выделить два отрезка локализации корней [1.5, 1.6] и [2.2, 2.4].

На втором этапе внутри выделенных отрезков вычисляются значения каждого из корней уравнения с заданной точностью. Для этого используются два основных итерационных подхода: последователь-

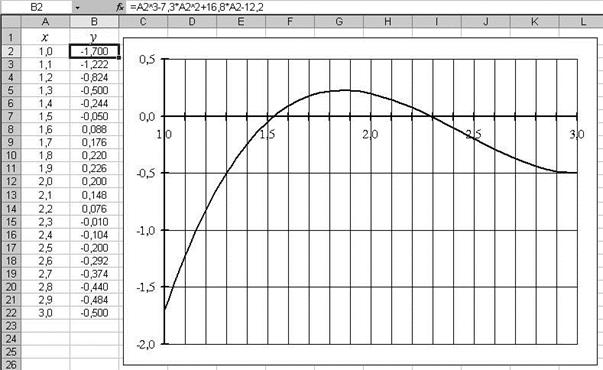
Рис.2.

ное уточнение первоначального приближения значения корня, взятого из выделенного отрезка, и сужение выделенного отрезка, содержащего корень.

-Метод Ньютона (I.Newton, 1669, Mr.Raphson, 1720)

В данном методе каждое новое приближение к значению корня уравнения f(x) = 0 ищется по следующей итерационной схеме

………………….

………………….

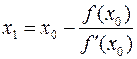
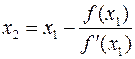
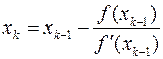
где x₀ – первоначальное приближенное значение корня, взятое с отрезка [a, b] локализации точного решения уравнения.

Если последовательность значений x_k (k = 0, 1, 2,...) сходится к точному значению корня x_т, то абсолютная погрешность значения корня на k-ом шаге (x_k) определяется выражением

, ,

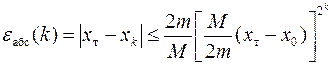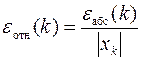где

, , , .

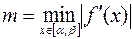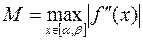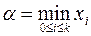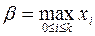Приведённые формулы для вычисления погрешностей требуют решения дополнительной задачи поиска минимума модуля первой производной функции f(x) и максимума модуля её второй производной на отрезке локализации корня [a, b]. В связи с этим на практике итерации завершают при выполнении одного из условий:

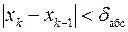или ,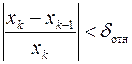

где δ_абс и δ_отн – задаваемые абсолютная и относительная разницы между соседними значениями приближения корня, соответственно. В этом случае надо помнить, что истинная погрешность определения корня может заметно отличаться от δ_абс или δ_отн. Поэтому после завершения поиска корня необходимо вычислить истинное значение погрешности решения по приведённым формулам для ε_абс или ε_отн.

Может случиться так, что последовательность приближённых значений x_k (k = 0, 1, 2, ...) корня x_т не имеет предела. В этом случае метод расходится, и описанная итерационная схема не может быть применена для решения уравнения. Анализ выражения для ε_абс позволяет сформулировать условие сходимости итераций. Очевидно, для того, чтобы погрешность ε_абс при стремлении k к бесконечности стремилась к нулю и итерации сходились к точному решению, надо обеспечить выполнение следующего неравенства

.

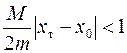При решении практических задач точное значение x_т корня уравнения неизвестно. Поэтому вместо приведённой формулы для абсолютной погрешности используют её аналоги

, ,

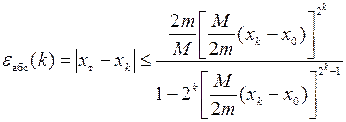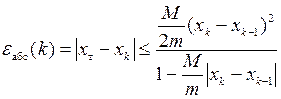где 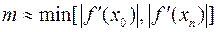, 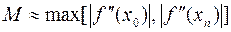в первом слу­чае и 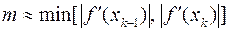, 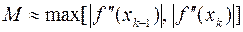во втором.

Для проверки итерационной схемы на сходимость применяется неравенство, подобное приведённому выше

,

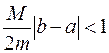где

, .

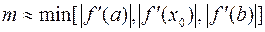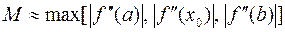При использовании этого неравенства надо помнить, что выбор значений границ отрезка локализации a и b существенно влияет на результаты проверки. Поэтому их надо выбирать так, чтобы они достаточно близки к x₀.

Графическая интерпретация работы метода Ньютона пред­ставлена на рис.3. Из точки на кривой y = f(x), имеющей абсциссу x₀, проводит 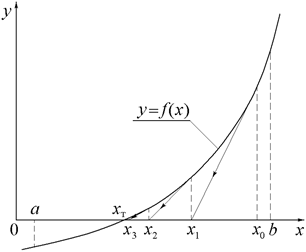ся касательная до пересечения с осью 0x. Абсцисса точки пересечения принимается за новое приближение значения x₁ корня уравнения f(x) = 0. В случае сходимости последовательности вычисляемых значений x₀, x₁,…, x_k,… процесс продолжается до тех пор, пока не выполнится условие его окончания.

Рассмотрим работу метода Ньютона на примере поиска приближённого значения корня уравнения

x³– 7.3x²+16.8x – 12.2 = 0

на отрезке [1, 2] и оценки погрешности его определения.

На первом этапе необходимо построить график левой части уравнения, для чего вычисляются её значения в трёх базовых точках

f(1.0) = 1.0³ – 7.3·1.0² + 16.8·1.0 – 12.2 = – 1.70,

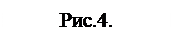f(1.5) = 1.5³ – 7.3·1.5² + 16.8·1.5 – 12.2 = – 0.05,

f(2.0) = 2.0³ – 7.3·2.0² + 16.8·2.0 – 12.2 = 0.20.

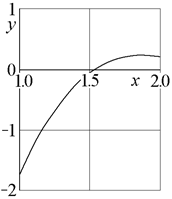
Как видно на рис.4, в качестве начального приближения корня рассматриваемого уравнения можно взять x₀= 1.5.

Теперь, следуя итерационной схеме метода Ньютона, можно вычислить первое приближение корня

,

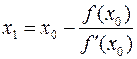где

f(x₀) = f(1.5) = 1.5³ – 7.3·1.5² + 16.8·1.5 – 12.2 = –0.05,

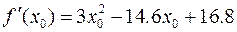= 3·1.5² – 14.6·1.5+16.8 = 1.65,

Отсюда получается значение корня в первом приближении

.

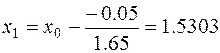Вторая итерация:

f(x₁)= 1.5303³ – 7.3·1.5303² + 16.8·1.5303 – 12.2 = –0.00254,

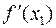= 3·1.5303² – 14.6·1.5303 + 16.8 = 1.48306,

.

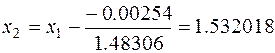Третья итерация:

f(x₂)= 1.532018³ – 7.3·1.532018² + 16.8·1.532018 – 12.2 = –8·10 ^–6,

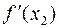= 3·1.532018² – 14.6·1.532018 + 16.8 = 1.47378,

.

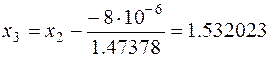Относительная разница между значениями приближения корня на второй и третьей итерациях составляет

.

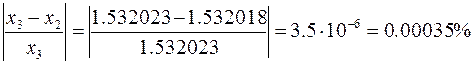Таким образом, если в задаче требовалось бы вычислить значение корня с относительной погрешностью ε_отн= 0.00001, то уточнение значения корня можно прекратить. Однако истинное значение абсолютной и относительной погрешностей требуется уточнить по формулам

, ,

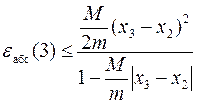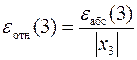где

, .

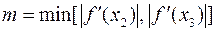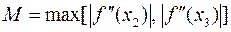Часть результатов известна, а остальные необходимо досчитать:

,

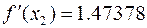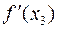= 3·1.5320232 – 14.6·1.532023 + 16.8 = 1.47375,

.

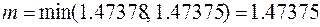Вторая производная функции имеет вид

,

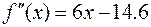откуда

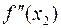= 6·1.532018 – 14.6 = –5.40789,

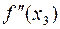= 6·1.532023 – 14.6 = –5.40786,

.

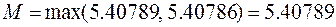Тогда абсолютная погрешность вычислений будет составлять

,

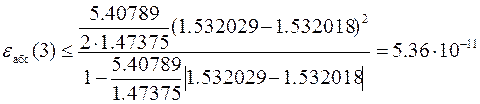а относительная примет значение

.

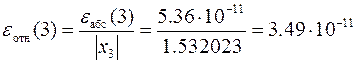Выполненные вычисления без определения истинного значения относительной погрешности могут быть сведены в таблицу 1:

Таблица 1.

i	xi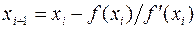
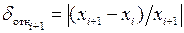
	x0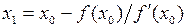
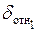
	x1
…	…..	…………	…..

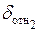
При реализации в программе Excel эта расчётная таблица метода Ньютона может быть представлена аналогичным образом. Ниже на рис.5 она приведена вместе с результатами расчетов.

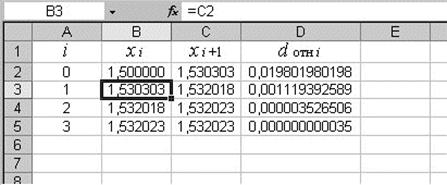
Рис.5.

Метод половинного деления (метод бисекций)

Алгоритм метода иллюстрируется на рис.6. Отрезок локализации [a, b] корня делится пополам x₁= (a + b)/2 и в полученной точке вычисляется значение функции. Если f(x₁) = 0, то корень найден и расчёты прекращают. В противном случае выбирается новый отрезок, содержащий корень уравнения, из отрезков [a, x₁] и [x₁, b]. На концах искомого отрезка функция f(x) должна иметь значения разного знака. Для это­го проверяется условие f(a) f(x₁) < 0. При его выполнении в качестве нового отрезка принимается отрезок [a, x₁], в противном случае – [x₁, b]. Процесс вычисления значения корня продолжается до тех пор, пока не будет выполнено требование к точности его определения. В данном случае оценка абсолютной погрешности определения корня

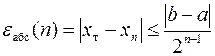
совпадает с длиной отрезка его последней локализации. В свою очередь относительная погрешность вычисляется как

.

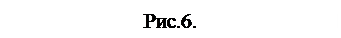
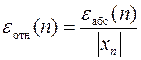При этом за значение корня принимается либо одна из границ суженного отрезка [a, b], либо его середина.

Алгоритм метода может быть проиллюстрирован на рассмотренном выше примере уточнения корня уравнения

x³– 7.3x²+16.8x – 12.2 = 0.

В качестве отрезка локализации выбирается отрезок [1.5, 1.6], содержащий первый корень уравнения (см. пример в описании метода Ньютона). На первом шаге уточнения корня вычисляются значения функции на границах выбранного отрезка

f(1.5) = 1.5³– 7.3·1.5²+ 16.8·1.5 – 12.2 = –0.05,

f(1.6) = 1.6³– 7.3·1.6²+ 16.8·1.6 – 12.2 = 0.088.

Затем в середине интервала x₁= 1.55 также вычисляется значение функции

f(1.55) = 1.55³– 7.3·1.55²+ 16.8·1.55 – 12.2 = 0.0256.

Так как эта точка не соответствует корню уравнения, то определяется новый отрезок его локализации. Для этого проверяется знак произведения значений функции на левой границы отрезка локализации корня и в его центре f(1.5)·f(x₁). Из расчётов видно, что это произведение меньше нуля, значит, в качестве нового отрезка локализации корня должен приниматься отрезок [1.5, 1.55].

Для выполнения второго шага уточнения корня значения функции на границах нового отрезка локализации считать не нужно, они уже известны: f(1.5) = –0.05; f(1.55) = 0.0256. Достаточно вычислить её значение в середине нового отрезка локализации корня x₂= 1.525

f(1.525) = 1.525³– 7.3·1.525²+ 16.8·1.525 – 12.2 = –0.0105.

Так как произведение f(1.5) f(x₂) больше нуля, то в качестве нового отрезка локализации принимается [1.525, 1.55]. Аналогично выполняются шаги c третьего по седьмой, дающие следующие значения приближения корня

x₃= 1.5375 – центр отрезка [1.525, 1.55],

x₄= 1.53125 – центр отрезка [1.525, 1.5375],

x₅= 1.53438 – центр отрезка [1.53125, 1.5375],

x₆= 1.53281 – центр отрезка [1.53125, 1.53438],

x₇= 1.53203 – центр отрезка [1.53125, 1.53281].

Значение относительной погрешности вычисления приближения x₇= 1.53203 корня уравнения будет определяться по формуле

.

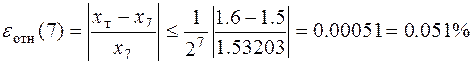Таким образом, если в задаче требовалось бы вычислить значение корня с относительной погрешностью ε_отн = 0.001-, то уточнение значения корня можно прекратить.

При реализации метода расчётная таблица может быть составлена в следующем виде:

Таблица 2.

i	ai	bi	f(ai)		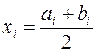f(xi)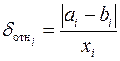
	a1	b1	f(a1)	x1	f(x1)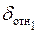
	Если f(a1)f(x1)<0, то a2 = a1, иначе a2 = x1.	Если f(a1)f(x1) 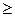0, то b2 = b1, иначе b2 = x1.	f(a2)	x2	f(x2)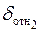
…	….………	…….……	……	…..	……	…….

Ниже на рис.7 представлены результаты расчётов в программе Excel.

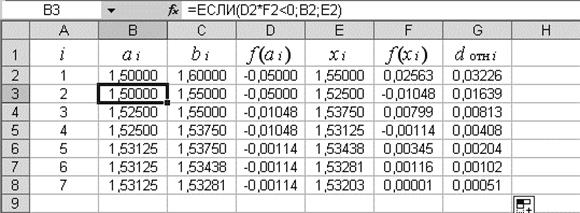
Рис.7.