Проверка гипотез с помощью непараметрических критериев
При решении многих теоретических и прикладных вопросов лингвистики, возникает необходимость рассмотреть характер распределения лигвистической генеральной совокупности. Эта задача решается путём проверки статистических гипотез о тождестве двух эмпирических распределений или об идентичности эмпирического и теоретического распределения. Для проверки непараметрических гипотез могут применяться различные критерии: критерий 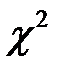 Пирсона, критерий Колмогорова-Смирнова, критерий асимметрии и эксцесса, графический способ, упрощённые критерии (критерий Романовского, числа Вестергарда, вариационная сетка Турбина) и т п.
Пирсона, критерий Колмогорова-Смирнова, критерий асимметрии и эксцесса, графический способ, упрощённые критерии (критерий Романовского, числа Вестергарда, вариационная сетка Турбина) и т п.
Критерий  Пирсона
Пирсона
Критерий Пирсона – наиболее часто употребляемый критерий для проверке гипотезы о законе распределения. Критерий основан на оценке отклонений эмпирических частот ni от теоретических  . Выборочное значение критерия, вычисляемое на основе выборочных данных, находится по формуле
. Выборочное значение критерия, вычисляемое на основе выборочных данных, находится по формуле 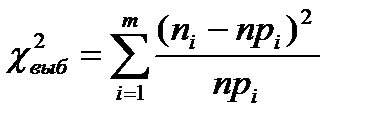 , где
, где 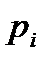 – теоретическая вероятность попадания значений нормально распределённой случайной величины в i-тый интервал.
– теоретическая вероятность попадания значений нормально распределённой случайной величины в i-тый интервал.
Пример: Статистическое распределение средних длин словоупотреблений 100 языков мира задано интеральным статистическим рядом:

| [2,6;3,4) | [3,4;4,2) | [4,2;5,0) | [5,0;5,8) | [5,8;6,6) | [6,6;7,4) | [7,4;8,2) | [8,2;9,0) |
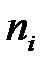
|
Можно ли среднюю длину словоупотребления использовать в качестве статистической характеристики для различения языков мира?
Если вариационный ряд средних длин словоформ близок к нормальному распределению, то средние длины словоформ плотнее группируются вокруг средней, задаваемой возможностями оперативной памяти человека. Отклонение от этой средней в каждом конкретном языке будет рассматриваться как результат случайных воздействий.
Для проверки степени соответствия полученного статистического распределения теоретическому нормальному закону воспользуемся критерием Пирсона.
1. Сформируем основную гипотезу H0: распределение средних длин словоформ можно считать нормальным. Тогда альтернативной будет гипотеза H1: распределение средних длин словоформ существенно отличается от нормального.
2. Необходимым условием применения критерия Пирсона является наличие в каждом из интервалов не менее 5 наблюдений. Так как число наблюдений в крайних интервалах меньше 5, объединим в статистическом ряде два первых и три последних интервала:
| Интервалы | [2,6;4,2) | [4,2;5,0) | [5,0;5,8) | [5,8;6,6) | [6,6;9,0) |
| частота ni |
3. Для дискретного статистического ряда, значениями которого являются середины интервалов, определимсреднее значение выборки 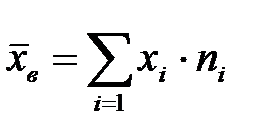 ;
; 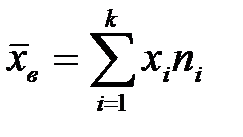 ;
; 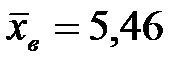 и исправленное среднее квадратическое отклонение
и исправленное среднее квадратическое отклонение 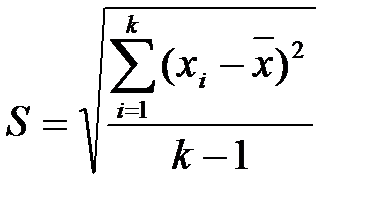 , S=1,11.
, S=1,11.
4. Так как нормально распределённая случайная величина определена на (-∞;∞), заменим крайние интервалы на интервалы (-∞;4,2) и [6,6;∞):

| (-∞;4,2) | [4,2;5,0) | [5,0;5,8) | [5,8;6,6) | [6,6;∞) |
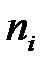
|
5. Вычислим теоретические вероятности попадания значений нормально распределённой случайной величины вполученные интервалы по формуле  где
где 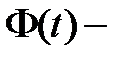 интегральная функция Лапласа, значения которой находим в таблице. При выполнении вычислений принимаем параметры теоретического распределения равными их оценкам, найденным по выборке, т.е.
интегральная функция Лапласа, значения которой находим в таблице. При выполнении вычислений принимаем параметры теоретического распределения равными их оценкам, найденным по выборке, т.е.  . Расчёты оформим в виде таблицы:
. Расчёты оформим в виде таблицы:

| (-∞; 4,2) | [4,2; 5,0) | [5,0; 5,8) | [5,8; 6,6) | [6,6; ∞) |
 эмпир. частота эмпир. частота
| |||||
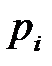 теор. вероятность теор. вероятность
| 0,125 | 0,212 | 0,285 | 0,229 | 0,149 |
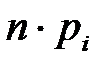 теоретич. частота теоретич. частота
| 12,5 | 21,2 | 28,5 | 22,9 | 14,9 |
6. Вычислим выборочное значение критерия 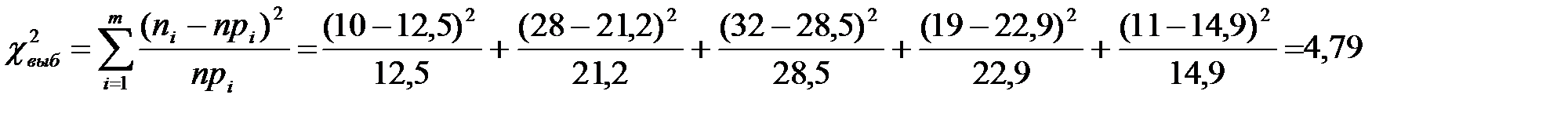 7. Выберем уровень значимости α =0,05. Рассчитаем k – число степеней свободы: k= m-r-1, k= 5-2-1, k= 2 (r - число параметров предполагаемого распределения, m – число интервалов). По таблице
7. Выберем уровень значимости α =0,05. Рассчитаем k – число степеней свободы: k= m-r-1, k= 5-2-1, k= 2 (r - число параметров предполагаемого распределения, m – число интервалов). По таблице 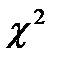 распределения находим критическую точку (квантиль)
распределения находим критическую точку (квантиль)  .
.
8. Так как  <
< 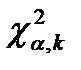 , то гипотеза H0 принимается, т.е. распределение средних длин словоформ языков мира можно считать нормальным
, то гипотеза H0 принимается, т.е. распределение средних длин словоформ языков мира можно считать нормальным
Ответ. Средняя длина словоформ не может считаться параметром для различения языков мира.
Часть 2. Вопросы и задания для практических работ.
Дата добавления: 2016-06-05; просмотров: 2453;











