Статистическая обработка результатов

Имеет две задачи:

1. Представить результаты многих определений в компактной форме – свертывание информации.

2. Оценить надежность результатов – степень их соответствия истинному содержанию элемента.

Случайные ошибки появляются по определенным законам, которые отражены в кривой нормального распределения Гаусса.

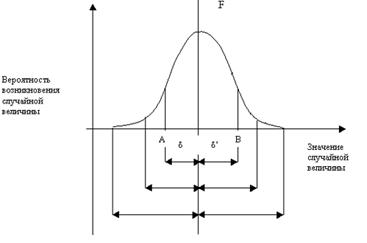
Практически вместо нормального распределения Гаусса

используют t-распределение Стьюдента, справедливое для малого объема выборки. Вместо истинного значения x₀ (которое редко известно) используют среднее арифметическое

.

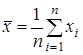Среднее арифметическое – сумма вариант, деленная на число вариант. Варианта – численное значение единичного определения.

Единичное отклонение (случайное отклонение):

.

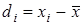Выборочный метод состоит в вычислении характеристик совокупности на основе наблюдения части ее элементов на основе случайного отбора. Малая выборка – выборка небольшого объема, менее 20÷30 единиц.

Стандартное (выборочное) отклонение малой выборки отдельного определения:

S= ,

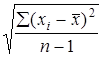отклонение среднего результата:

.

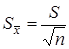Квадрат отклонения называют дисперсией.

S² – выборочная дисперсия отдельного определения;

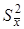– выборочная дисперсия среднего значения, служащая для оценки воспроизводимости.

Для малых выборок для определения границ доверительного интервала используют t-распределение Стьюдента

,

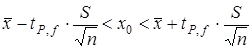где t_p,f – коэффициент Стьюдента (коэффициент нормированного отклонения) для данной доверительной вероятности P и вариантности f=n-1.

Истинное значение x₀ или генеральное среднее находится в пределах, которые называются доверительные границы.