Точечные оценки математического ожидания, дисперсии и вероятности.
Точечная оценка – оценка 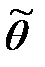 , которую используют в качестве приближённого значения параметра
, которую используют в качестве приближённого значения параметра 
 Пусть
Пусть 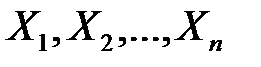 – выборка, полученная в результате n независимых наблюдений за СВ Х (чтобы подчеркнуть случайный характер, значения выборки обозначаются прописными буквами). Случайные величины
– выборка, полученная в результате n независимых наблюдений за СВ Х (чтобы подчеркнуть случайный характер, значения выборки обозначаются прописными буквами). Случайные величины 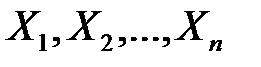 можно рассматривать как n одинаково распределенных случайных величин, поэтому все СВ имеют одинаковые М(Х) и дисперсии:
можно рассматривать как n одинаково распределенных случайных величин, поэтому все СВ имеют одинаковые М(Х) и дисперсии:
Тогда:
– среднее выборочное 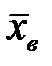 есть несмещённая и состоятельная оценка математического ожидания М(Х) генеральной совокупности;
есть несмещённая и состоятельная оценка математического ожидания М(Х) генеральной совокупности;
– исправленная выборочная дисперсия 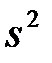 есть несмещённая и состоятельная оценка дисперсии D(X) генеральной совокупности.
есть несмещённая и состоятельная оценка дисперсии D(X) генеральной совокупности.
- относительная частота 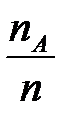 появления события А в n независимых испытаниях есть несмещённая, состоятельная и эффективная оценка вероятности события А.
появления события А в n независимых испытаниях есть несмещённая, состоятельная и эффективная оценка вероятности события А.
Задача 3.Для анализа лингвистических терминологических систем взято 7 фрагментов по 250 терминоупотреблений из русских лингвистических текстов. После подсчёта в каждом фрагменте числа употреблений слова «лицо» получен следующий вариационный ряд: 1,1,3,4,9,10,12.
1. Определите по выборке несмещённую и состоятельную оценку математического ожидания М(Х) и дисперсии D(X) случайной величины Х - «число употреблений слова «лицо» в русских лингвистических текстах.
2. Найдите несмещённую, состоятельную и эффективную оценку вероятности события А= «слово лицо использовано более 5 раз».
Решение 1.Несмещённая и состоятельная оценка М(Х) есть среднее выборочное 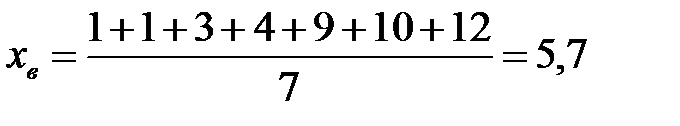 .
.
Несмещённая и состоятельная оценка D(X) есть исправленная выборочная дисперсия:
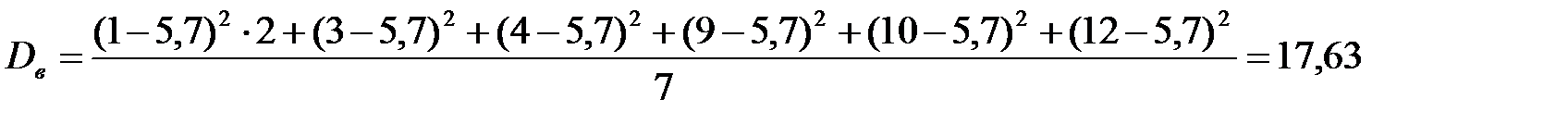
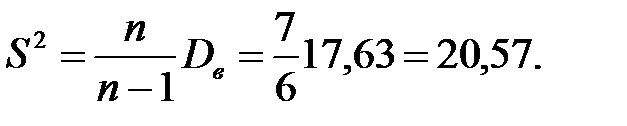
2. Несмещённой, состоятельной и эффективной оценкой вероятности события А= «слово лицо использовано более 5 раз» является частота этого события: Р(А): 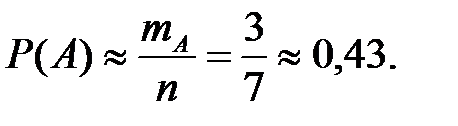
Дата добавления: 2016-06-05; просмотров: 2151;











