ЛЕКЦИЯ 12. Обоснование несуществования эффективного алгоритма в классе задач распознавания свойств

Инфы

Перейдем к рассмотрению важного технического результата. Некоторые универсальные в классе NP задачи формализуются через условие вида:

,

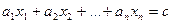(12.1)

где , с – целые и положительные;

.

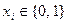В частности, такова задача об упаковки в контейнер (ЗУК). Частный вид (12.1) входит в задачу о минимальном покрытии 0,1 – матрицы. Сформулируем проблемы: «Можно ли ЗУК свести к эквивалентной задаче Выполнимость, записанной на том же множестве переменных, так, чтобы для любого n размеры задачи Выполнимость (коротко ВЫП), были ограничены некоторым фиксированным полиномом от n?»

Ответ на поставленную проблему дает теорема 6.

Теорема. Невозможно сведение ЗУК 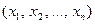к ВЫП 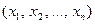с сохранением свойства эквивалентности множества решений, при котором для каждого n размеры ВЫП 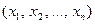были бы ограничены некоторым фиксированным полиномом от n.

В частности, эквивалентная ВЫП для условия

,

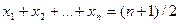(12.2)

где n – четное требует минимальной КНФ с 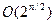дизъюнктами, т.е. размеры ВЫП растут экспоненциально.

Этот технический результат дает нам следующее.

Покажем, как для (12.2) построить H-эквивалентную КНФ полиномиальных от n размеров. Этот общий способ продемонстрируем для уравнения

.

Будем использовать дополнительные булевские переменные 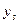, , 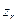…, 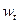( 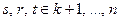) и имея в виду :

,

,

…

,

,

,

…

.

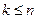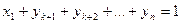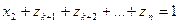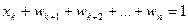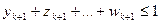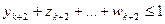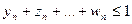В приведенной системе нет основных переменных 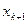, , 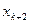…, 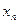. Они выражаются через дополнительные переменные следующим образом:

, , … .

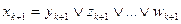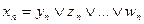(12.3)

Нетрудно показать, что полученная расширенная система потребует 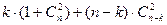дизъюнктов. В самом деле, условие

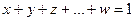
передается системой

…

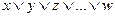
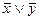
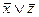
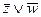
Условие

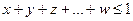
передается такой же системой, но без дизъюнкта .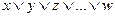

Итак, полученную полиномиальную по размерам КНФ для (12.4) назовем Н-КНФ, а первоначальную минимальную КНФ экспоненциальных размеров, назовем Э-минКНФ.

Имеет место утверждение: Э-минКНФ и Н-КНФ суть H-эквивалентные задачи и

.

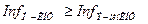Доказательство. H-эквивалентность следует непосредственно по определению: любое решение Н-КНФ содержит решение Э-минКНФ. Наоборот, любое решение Э-минКНФ может быть достроено до решения Н-КНФ в силу (12.3).

Таким образом, мы видим, что полиномиальная по размеру записи КНФ может содержать экспоненциальное число инфов. Таким образом, любой реалистический алгоритм, который выполняет учет индивидуальных инфов, потратит экспоненциально растущее число шагов на решение задачи. Таким образом, только использование форм может дать надежду на преодоление экспоненциальной сложности. Однако , скорее всего, это невозможно.

Итак, сформулируем основные идеи проведенного нами рассмотрения. Мы показали, что имеются полиномиальные от n (n – число переменных) задачи ВЫП, локализующие в себе экспоненциальное число инфов. Имеется H-эквивалентная КНФ для таких ВЫП, которая содержит экспоненциальное число дизъюнктов. Таким образом, в силу постулата об ограниченной пропускной способности алгоритма нужно затратить экспоненциальное число тактов, чтобы принять во внимание каждый инф индивидуально. Следовательно, чтобы число тактов вычислителя было полиномиальным, нужно либо игнорировать инфы (чего не допускают реалистические алгоритмы), либо принимать во внимание целые блоки инфов, т.е. формы. Анализ этой возможности, однако, выходит за пределы данного курса.

ЛИТЕРАТУРА

1. Пападимитриу Х., Стайглиц К. Комбинаторная оптимизация. М., Мир, 1985, - 510с.

2. Герман О.В. Введение в теорию экспертных систем и обработку знаний. Мн., ДизайнПро, 1995.- 256с.

3. Гэри М., Джонсон Д. Вычислительные машины и труднорешаемые задачи. М., Мир, 1982 – 356с.

4. Герман О.В., Гончарова Е.Н. Об одной концепции вычислительной сложности. Вестник ставропольского гос. Университета. Вып. 40, 2006, с.16-24.