Решение сеточных уравнений.

Модельная задача, положим в (11.1) .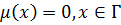

Отметим, что каждое уравнение системы (11.2) для модельной задачи содержит не более пяти отличных от нуля коэффициентов. Мы имеем дело с так называемой сильно разреженной матрицей системы. Причём, ненулевые коэффициенты сосредоточены рядом с главной диагональю матрицы.

Метод простой итерации для дискретизации модельной задачи:

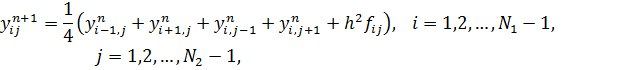
Можно показать, что метод Якоби требует 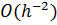итераций для достижения заданной точности. Это очень медленная сходимость. В настоящее время применяются методы, требующие 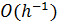и даже 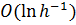итераций для достижения той же точности.

Рассмотрим метод Зейделя для дискретизации модельной задачи. В общем случае Реализация метода Зейделя для приводит к следующему итерационному методу:

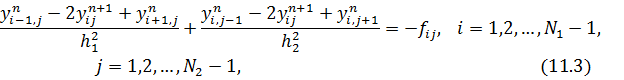
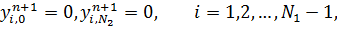
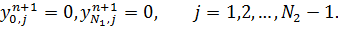
Хотя метод Зейделя является неявным, нахождение значений 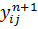на новой итерации не представляет труда, поскольку оно сводится к обращению треугольной матрицы. Здесь нужно лишь правильно установить последовательность проведения вычислений.

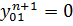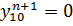Сначала из уравнения (11.3), используя известные граничные значения и , находят 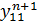. Зная 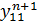, можно найти 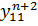и т. д. Таким образом, неизвестные 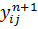вычисляются в следующем порядке изменения индексов: (1,1), (1,2),..., (1,N-1), (2, 1), (2, 2),..., (2, N-1), .... (N-1, 1), (N-1, 2),..., (N-1, N-1). В этом случае говорят, что вычисления ведутся от левого нижнего угла прямоугольника G к правому верхнему углу.

Можно показать, что метод Зейделя сходится несколько быстрее, чем метод Якоби, однако число итераций, необходимое для достижения заданной точности, здесь также является величиной порядка .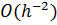

1.