Интервальные оценки для генеральной дисперсии и среднего квадратического отклонения
Пусть из генеральной совокупности Х, распределённой по нормальному закону 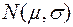 , взята случайная выборка объёмом n и вычислена выборочная дисперсия
, взята случайная выборка объёмом n и вычислена выборочная дисперсия 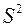 . Требуется определить с надёжностью
. Требуется определить с надёжностью 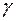 интервальную оценку генеральной дисперсии
интервальную оценку генеральной дисперсии 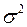 .
.
Построение доверительного интервала основано на том, что случайная величина 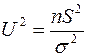 имеет распределение Пирсона
имеет распределение Пирсона 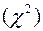 с
с 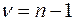 степенями свободы.
степенями свободы.
Для уровня значимости 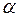 можно записать доверительную вероятность
можно записать доверительную вероятность
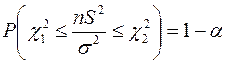
Границы доверительного интервала 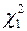 и
и 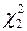 обычно выбирают так, чтобы
обычно выбирают так, чтобы
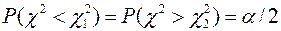
Тогда имеем
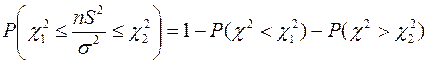 (10)
(10)
Так как таблица 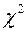 - распределения содержит лишь критические значения для правосторонних критических областей, т.е
- распределения содержит лишь критические значения для правосторонних критических областей, т.е 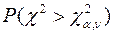 , то для вычисления левой границы
, то для вычисления левой границы 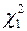 запишем тождество:
запишем тождество:
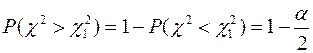 (11)
(11)
Правую границу доверительного интервала 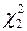 найдём из равенства
найдём из равенства
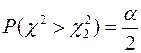 (12)
(12)
С учётом формулы (11) равенство (10) примет вид
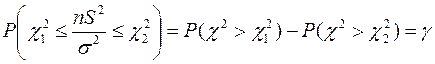 (13)
(13)
Формула (13) используется при решении обратной задачи- нахождении доверительной вероятности по заданному доверительному интервалу.
Из неравенства
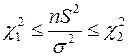
получаем интервал для генеральной дисперсии
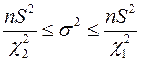 . (14)
. (14)
Доверительный интервал для генерального среднего квадратического отклонения 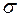 при
при 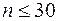 равен
равен
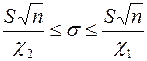 (15)
(15)
При достаточно больших объёмах выборки 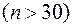 доверительный интервал определяется неравенством:
доверительный интервал определяется неравенством:
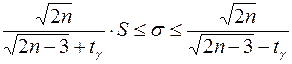 , (16)
, (16)
где 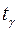 определяется из уравнения
определяется из уравнения 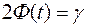 .
.
Пример 2. По результатам контроля 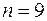 деталей вычислено выборочное среднее квадратическое отклонение
деталей вычислено выборочное среднее квадратическое отклонение 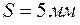 . В предположении, что ошибка изготовления деталей распределена по нормальному закону, определить с надёжностью
. В предположении, что ошибка изготовления деталей распределена по нормальному закону, определить с надёжностью 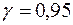 доверительный интервал для параметра
доверительный интервал для параметра 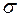 .
.
Решение: Так как 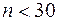 , используется
, используется 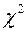 - распределение. Согласно формулам (11) и (12), имеем:
- распределение. Согласно формулам (11) и (12), имеем:
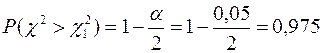 ,
,
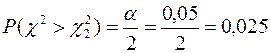 .
.
По таблице 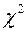 - распределения для числа степеней свободы
- распределения для числа степеней свободы 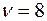 и найденных вероятностей 0,975 и 0,025 находим
и найденных вероятностей 0,975 и 0,025 находим 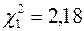 ,
, 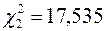 .
.
Вычисляем 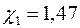 и
и 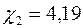 . Доверительный интервал по формуле (15) равен
. Доверительный интервал по формуле (15) равен
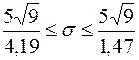
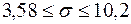 .
.
Дата добавления: 2021-12-14; просмотров: 409;











