Вывод дифференциальных уравнений
Статистические характеристики системы АРДС можно рассмотреть, если в координатах напряжение - ток совместить вольт-амперную характеристику питающей системы 1 со статической характеристикой устойчивого горения дуги 2 (рис.2.1.4).
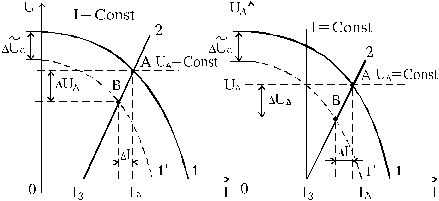
Рис.2.1.4. Совмещенные характеристики вольтамперные источника
питания 1 и устойчивого горения дуги 2 в системе АРДС
Уравнение статической характеристики устойчивого горения дуги как регулируемого объекта может быть определено совместным решением диффуравнений:
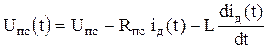 , (2.1.2)
, (2.1.2)
Uд(t)=U0д+kдlд+Rдiд(t), (2.1.3)
где Unc и U0д - некоторые напряжения, полученные в результате линеаризации статической внешней характеристики источника питания и статической вольт-амперной характеристики дуги;
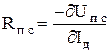 - динамическое сопротивление источника питания, соответствующее рассматриваемой точке внешней характеристики;
- динамическое сопротивление источника питания, соответствующее рассматриваемой точке внешней характеристики;
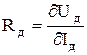 - динамическое сопротивление дуги;
- динамическое сопротивление дуги;
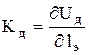 - градиент напряжения в столбе дуги;
- градиент напряжения в столбе дуги;
lэ - длина дуги;
L - индуктивность источника питания.
Скорость изменения длины дугового промежутка определяется разностью скоростей плавления и подачи электродной проволоки
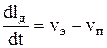 .
.
Для упрощения анализа примем, что скорость плавления электрода является линейной функцией тока дуги
vэ=kстiд-a.
Учитывая, что Unc=Uд и решая полученные уравнения относительно тока, получим
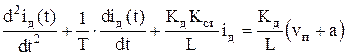 , (2.1.4)
, (2.1.4)
где 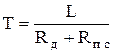 .
.
Дата добавления: 2021-12-14; просмотров: 592;











