Критерий устойчивости Михайлова
Применение критерия устойчивости Гурвица для систем с характеристическим уравнением выше 4-го порядка затруднено.
Частотный критерий устойчивости А.М.Михайлова позволяет судить об устойчивости систем любого порядка по виду ее характеристического вектора (годографа) на комплексной плоскости. Годограф Михайлова получают подстановкой P=jw в характеристический полином характеристического уравнения и построением кривой в координатах U(w) и jV(w) при изменении w от 0 до ¥
D(jw)=U(w)+jV(w)=a0(jw)n + a1(jw)n-1+...+ an-1(jw)+an . (1.6.18)
Определение критерия Михайлова. Для устойчивости САУ необходимо и достаточно, чтобы ее характеристический вектор при изменении частоты от 0 до ¥ повернулся против часовой стрелки, начиная с положительной вещественной оси и проходя последовательно такое количество квадрантов на координатной плоскости, которое равно порядку характеристического уравнения, т.е. угол поворота должен быть np/2.
На рис.1.6.4,а показаны кривые устойчивых систем, а на рис.1.6.4,б - неустойчивых систем.
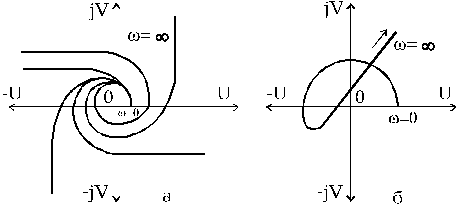
Рис.1.6.4. Кривые Михайлова:
а - устойчивые системы; б - неустойчивые системы
Пример. Оценим устойчивость системы третьего порядка с передаточной функцией (1.5.5) и характеристическим уравнением (1.6.15)
D(jw)=(К-(T1+T2)w2)+j(w(1-T1T2w2)). (1.6.19)
Построим кривую Михайлова (рис.1.6.5).
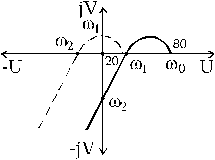
рис.1.6.5. Кривые Михайлова системы
третьего порядка
При V=0 получим 1-T1T2w2 =0
или 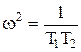 . (1.6.20)
. (1.6.20)
При U=0 получим К-(T1+T2)w2=0 (1.6.21)
или 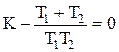 . (1.6.22)
. (1.6.22)
Отсюда 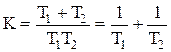 , что аналогично и критерию Гурвица (1.6.17).
, что аналогично и критерию Гурвица (1.6.17).
Другая форма критерия Михайлова состоит в использовании свойства перемежаемости корней многочленов U(w) и V(w), т.е. корни U(w)=0 и V(w)=0 должны поочередно следовать друг за другом. На рис. 1.6.5 w0=0; w1>w2 или из (1.6.20) и (1.6.21) имеем:
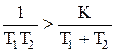 .
.
Дата добавления: 2021-12-14; просмотров: 419;











