Интегрирующие и дифференцирующие цепи

В импульсных устройствах задающий генератор часто вырабатывает импульсы прямоугольной формы определенной длительности и амплитуды, которые предназначаются для представления чисел и управления элементами вычислительных устройств, устройств обработки информации и др. Однако для правильного функционирования различных элементов в общем случае требуются импульсы вполне определенной формы, отличной от прямоугольной, имеющие заданные длительность и амплитуду. Вследствие этого возникает необходимость предварительно преобразовывать импульсы задающего генератора. Характер преобразования может быть разным. Так, может потребоваться изменить амплитуду или полярность, длительность задающих импульсов, осуществить их задержку во времени.

Преобразования в основном осуществляются с помощью линейных цепей — четырехполюсников, которые могут быть пассивными и актив­ными. В рассматриваемых цепях пассивные четырехполюсники не содер­жат в своем составе источников питания, активные используют энергию внутренних или внешних источников питания. С помощью линейных цепей осуществляются такие преобразования, как дифференцирование, интегрирование, укорочение импульсов, изменение амплитуды и поляр­ности, задержка импульсов во времени. Операции дифференцирования, интегрирования и укорочения импульсов выполняются соответственно дифференцирующими, интегрирующими и укорачивающими цепями. Изменение амплитуды и полярности импульса может производиться с помощью импульсного трансформатора, а задержка его во времени — линией задержки.

Интегрирующая цепь. На рис. 19.5 приведена схема простейшей цепи (пассивного четырехполюсника), с помощью которой можно выпол
нить операцию интегрирования входного электрического сигнала, подан­ного на зажимы 1-1^|, если выходной сигнал снимать с зажимов 2-2'.

Составим уравнение цепи для мгновенных значений токов и напря­жений по второму закону Кирхгофа:

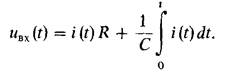
Отсюда следует, что ток цепи будет изменяться по закону

Если выбрать постоянную времени достаточно большой, то вторым слагаемым в последнем уравнении можно пренебречь, тогда i(t) = u_вх(t)/R.

Напряжение на конденсаторе (на зажимах 2-2') будет равно

(19.1)

Из (19.1) видно, что цепь, приведенная на рис. 19.5, выполняет опе­рацию интегрирования входного напряжения и умножения его на коэф­фициент пропорциональности, равный обратному значению постоянной времени цепи:

Временная диаграмма выходного напряжения интегрирующей цепи при подаче на вход последовательности прямоугольных импульсов показана на рис. 19.6.

Дифференцирующая цепь. С помощью цепи, схема которой приведена на рис. 19.7 (пассивного четырехполюсника), можно выполнять операцию дифференцирования входного электрического сигнала, поданного на зажимы 1-1', если выходной сигнал снимать с зажимов 2-2'. Составим уравнение цепи для мгновенных значений тока и напряжений по второму закону Кирхгофа:

Если сопротивление R мало и членом i(t)R можно пренебречь, то ток в цепи 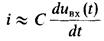и выходное напряжение цепи, снимаемое с R,

(19.2)

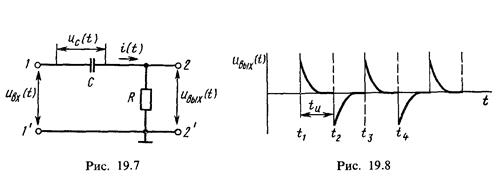
Анализируя (19.2), можно видеть, что с помощью рассматриваемой цепи выполняют операции дифференцирования входного напряжения и умножения его на коэффициент пропорциональности, равный постоян­ной времени τ = RC. Форма выходного напряжения дифференцирующей цепи при подаче на вход серии прямоугольных импульсов приведена на рис. 19.8. В этом случае теоретически выходное напряжение должно представлять собой знакопеременные импульсы бесконечно большой амплитуды и малой (близкой к нулю) длительности.

Однако вследствие различия свойств реальной и идеальной диф­ференцирующих цепей, а также конечной крутизны фронта импульса на выходе получают импульсы, амплитуда которых меньше амплитуды входного сигнала, а длительность их определяется как t_и = (3 ÷ 4) τ = (3 ÷ 4)RС.

В общем случае форма выходного напряжения зависит от соотно­шения длительности импульса входного сигнала t_и и постоянной вре­мени дифференцирующей цепи τ. В момент t₁ входное напряжение при­ложено к резистору R, так как напряжение на конденсаторе скачком изменяться не может. Затем напряжение на конденсаторе возрастает по экспоненциальному закону, а напряжение на резисторе R, т. е. выходное напряжение, снижается по экспоненциальному закону и становится рав­ным нулю в момент t₂, когда зарядка конденсатора закончится. При малых значениях τ длительность выходного напряжения мала. Когда напряжение u_BX(t) становится равным нулю, конденсатор начинает разряжаться через резистор R. Таким образом формируется импульс обратной полярности.

Пассивные интегрирующие и дифференцирующие цепи имеют сле­дующие недостатки: обе математические операции реализуются прибли­женно, с известными погрешностями. Приходится вводить корректи­рующие звенья, которые, в свою очередь, сильно снижают амплитуду выходного импульса, т. е. без промежуточного усиления сигналов практически невозможны n-кратные дифференцирование и интегриро­вание.

Эти недостатки не свойственны активным дифференцирующему и интегрирующему устройствам. Одним из возможных способов реали­зации этих устройств является применение операционных усилителей (см. гл. 18).

Активное дифференцирующее устройство. Схема такого устройства на операционном усилителе приведена на рис. 19.9. Ко входу 1 подключен конденсатор С, а в цепь обратной связи включен резистор R_oc. Так как входное сопротивление чрезвычайно велико (R_вх -> ∞), то входной ток обтекает схему по пути, указанному пунктиром. С другой сторо­ны, напряжение и_вхОУ в этом включении очень мало, так как К_u -> ∞, поэтому потенциал точки В схемы практически равен нулю. Следовательно, ток на входе

(19.3)

Ток на выходе i(t) одновременно является зарядным током кон­денсатора С: dq= Сdu _BX (t), откуда

(19.4)

Приравнивая левые части уравнений (19.3) и (19.4), можно написать -и_вых(t)/R_oc = С du_вх (t)/dt, откуда

(19.5)

Таким образом, выходное напряжение операционного усилителя является произведением производной входного напряжения по времени, умноженной на постоянную времени τ = R_ОСС.

Активное интегрирующее устройство. Схема интегрирующего устройст­ва на операционном усилителе, приведенная на рис. 19.10, отличается от дифференцирующего устройства рис. 19.9 только тем, что конденсатор С и резистор R_oc (на рис. 19.10 —R₁) поменялись местами. По-прежнему R_вх -> ∞ и коэффициент усиления по напряжению К_u -> ∞. Следовательно, в устройстве конденсатор С заряжается током i(t) =u_BX(t)/R₁. Так как напряжение на конденсаторе практически равно выходному напряжению (φ_B = 0), а операционный усилитель изменяет фазу входного сигнала на выходе на угол π, имеем

(19.6)

Таким образом, выходное напряжение активного интегрирующего устройства есть произведение определенного интеграла от входного напряжения по времени на коэффициент 1/τ.

Линии задержки

Во многих элементах электроники, автоматики и особенно в счетно-решающей технике часто требуется задерживать импульс на какое-то время t (время задержки) относительно какого-нибудь опорного (время его появления идентифицируется с нулевым моментом) импульса. Устройства, задерживающие выходной импульс относительно входного, называются линиями задержки (ЛЗ). Линии задержки могут быть естественными и искусственными.

Простейшей искусственной ЛЗ могут быть RC- или .RL-цепи (рис. 19.11, а, б), которые питаются от генератора прямоугольных им­пульсов (ГПИ). В обеих указанных цепях выходной импульс в точках 2-2' задерживается относительно входного импульса (точки 1-1^’) на t_з = (2 ÷ 3)τ (рис. 19.12). С помощью пороговых устройств можно очень точно зафиксировать t_з.

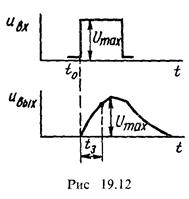К недостаткам таких устройств следует отнести большое искажение импульса и особенно удлинение фронтов.

В сверхбыстродействующих электронных устройствах применяются искусственные ЛЗ. Одна из таких ЛЗ приведена на рис. 19.13, a. Такая многозвенная линия обладает дисперсией времени задержки импульсов, связанной с зависимостью параметров отдельных звеньев от частоты импульсов. Емкость С является постоянной, а индуктивность — пере­менной. Индуктивные катушки выполнены на ферритовых кольцах. Процессы, происходящие в такой нелинейной дискретной ЛЗ при передаче импульса, описываются нелинейными дифференциальными уравнениями, общее исследование которых достаточно сложное. Рас­смотренная ЛЗ обеспечивает задержку импульса на время не меньшее, чем длительность фронта входного импульса, и дает возможность получать задержанный импульс с крутым фронтом и значительной амплитудой на низкоомной нагрузке.

На рис. 19.13,б приведена схема линейной ЛЗ. Длительность задержки одного звена (пунктир на рисунке) t_l определяется производ­ной фазочастотной характеристики:

(19.7)

где ω_с =2/ — частота среза. Если соблюдается предположение, что частоты, составляющие спектр сигнала, малы по сравнению с ω_с, то t_з = n , где n — число звеньев ЛЗ. Однако при подаче через ЛЗ перепадов напряжений необходимо считаться с неизбежными искажениями фронтов импульсов. Теорети­ческие и экспериментальные исследования показывают, что при идеаль­ном скачке напряжения U₀ на входе ЛЗ длительность фронта выход­ного напряжения для одного звена при согласованной нагрузке, когда R_H = ρ, где ρ — волновое сопротивление ЛЗ, составляет t_ф1 ≈ 1,13 , а для n-звенной ЛЗ — в n^1/3 раз больше, т. е.

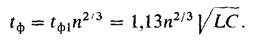(19.8)

Длительность задержки, отсчитанной от момента подачи входного импульса, до момента, когда напряжение на выходе достигает 0,5U₀, оказывается для одного звена равной

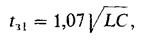(19.9)

а для n-звенной ЛЗ

(19.10)

Для высокоомных нагрузок пригодна ЛЗ с использованием сегнето-электрика (рис. 19.14), которая состоит из звеньев, содержащих катушку постоянной индуктивности L и нелинейную емкость С (u) в виде конден­саторов с сегнетоэлектриком. Зависимость емкости этих конденсаторов от напряжения обусловлена тем, что диэлектрическая проницаемость у сегнетоэлектрика есть функция напряженности электрического поля ε = f(E). Такие конденсаторы называют варикондами. Задержка импуль­са в линии может достигать значений t_з = nt₁, где n — число звеньев.

Более перспективным, однако, является применение искусственных ЛЗ с полупроводниками. Такая ЛЗ выполняется в виде звеньев с постоян­ной индуктивностью L и нелинейной емкостью С (u) (рис. 19.15). В качестве нелинейной емкости используют варикапы, емкость которых изменяется при изменении обратного напряжения.

Все рассмотренные ЛЗ могут быть использованы и как форми­рующие нелинейные цепи для импульсов с фронтами длительностью в сотые доли наносекунды.