Динамика двигателя ПТ с учетом индуктивности якоря

Будем рассматривать от момента пуска: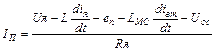

t₃ – время запаздывания

e_n – противо ЭДС (создается изменением скорости)

ЭДС самоиндукции (создается изменением тока)

L_МС – магнитные системы (весь магнитопровод, нелинейный и неоднородный)

i_вт – вихревые токи

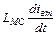- ЭДС магнитной системы

U_ос – напряжение обратной связи по скорости

Работает: .

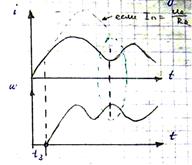
Если 4T_я>T_M, то возникают колебания за счет перерастания колебаний мех. системы в колебания Эл-м. Системы и наоборот

Фазовый портрет двигателя постоянного тока:

31 Переходной процесс двигателя w=f(t) с учетом индуктивности якоря

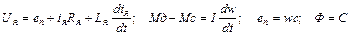
Здесь 2-а источника инерционности: I и L.

Мы пренебрегаем Мс – идеальный холостой ход

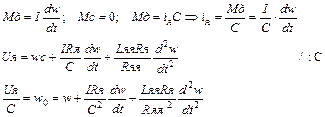
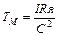- эл. мех. постоянная

- постоянная времени обмотки якоря

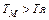- всегда!

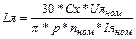, где Сх=0,4 – если система без компенсационной обмотки; Сх=0,1 - если система с компенсационной обмоткой.

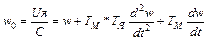
Решением этого уравнения является: 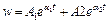, где a₁, a₂ – корни характеристического уравнения: .

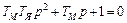Постоянная интегрирования A₁, A₂ находятся из начальных условий t=0 и .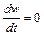

Решение: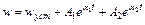

- для расчета переходного процесса