Параметры зацепления, составленного из эвольвентных колес, нарезанных со смещением исходного контура
Угол зацепления 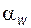 и межосевое расстояние
и межосевое расстояние 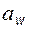 при беззазорном зацеплении
при беззазорном зацеплении
Начальные окружности диаметров 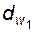 и
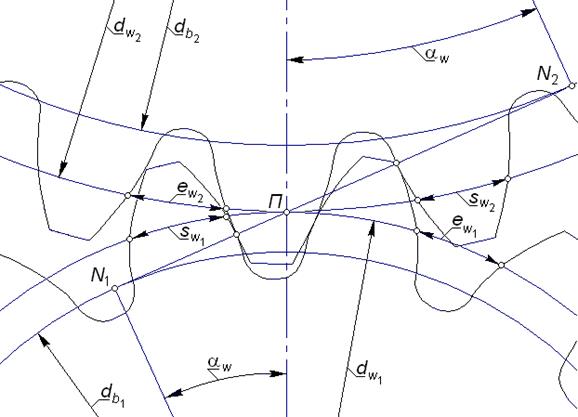
и 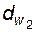 (рис. 5.11) перекатываются друг по другу без скольжения, следовательно, окружные шаги зубьев по дугам начальных окружностей(начальные окружные
(рис. 5.11) перекатываются друг по другу без скольжения, следовательно, окружные шаги зубьев по дугам начальных окружностей(начальные окружные
шаги 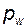 ) для обоих колес одинаковы и равны
) для обоих колес одинаковы и равны
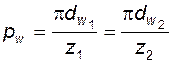 ; (5.29)
; (5.29)
также одинаковы для обоих колес углы профиля на начальных окружностях: они равны углу зацепления 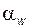 .
.
Если в зацеплении возможен свободный поворот одного из колес при неподвижном парном колесе, то говорят, что имеет место зацепление с боковым зазором. Очевидно, что при беззазорном зацеплении (зацеплении без бокового зазора) толщина зуба 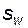 по дуге начальной окружности каждого из колес равна ширине впадины
по дуге начальной окружности каждого из колес равна ширине впадины 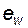 парного колеса, т.е.
парного колеса, т.е. 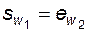 и
и 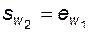 . Но поскольку
. Но поскольку 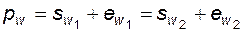 , то условие, при соблюдении которого зацепление двух колес является беззазорным, принимает вид
, то условие, при соблюдении которого зацепление двух колес является беззазорным, принимает вид
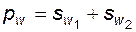 . (5.30)
. (5.30)
Тогда, согласно (5.23)
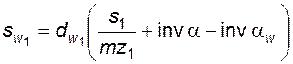 ; (5.31)
; (5.31)
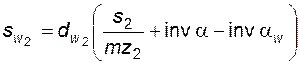 . (5.32)
. (5.32)
|
| Рис. 5.11 |
Подставляя (5.29), (5.31) и (5.32) в (5.30), из полученного выражения найдем
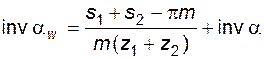 , (5.33)
, (5.33)
или, принимая во внимание формулу (5.15),
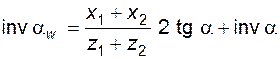 . (5.34)
. (5.34)
Равенства (5.33) и (5.34) определяют угол зацепления 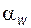 , при котором колеса, имеющие делительные толщины зубьев
, при котором колеса, имеющие делительные толщины зубьев 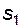 и
и 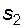 (или нарезанные при коэффициентах смещения
(или нарезанные при коэффициентах смещения 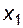 и
и 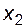 ), зацепляются без бокового зазора; указанные равенства равносильны.
), зацепляются без бокового зазора; указанные равенства равносильны.
Сумму коэффициентов смещения в (5.34) часто обозначают, как 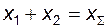 и называют коэффициентом суммы смещений.
и называют коэффициентом суммы смещений.
Таким образом, из формулы (5.34) (или (5.33)) находят угол беззазорного зацепления 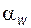 .
.
Межосевое расстояние связано с углом зацепления формулой (5.7); из нее следует, что
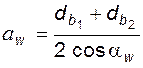 , (5.35)
, (5.35)
или, с учетом (5.14),
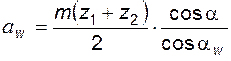 . (5.36)
. (5.36)
Таким образом, межосевое расстояние 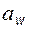 при беззазорном зацеплении можно найти из (5.36), если в нее подставить
при беззазорном зацеплении можно найти из (5.36), если в нее подставить 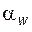 , найденное с помощью (5.33) или (5.34).
, найденное с помощью (5.33) или (5.34).
В дальнейшем будем считать, что при отсутствии дополнительных указаний межосевое расстояние рассчитывают, исходя из беззазорного зацепления.
Диаметры окружностей вершин колес (диаметры вершин)
|
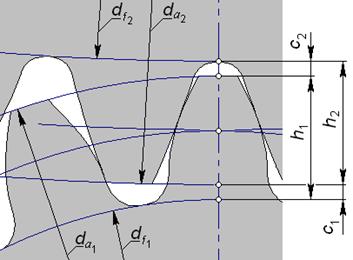
| Рис. 5.12 |
Поверхность вершин зубчатого колеса (в отличие от поверхности впадин) не обрабатывается при нарезании зубьев и диаметр вершин может назначаться в некоторых пределах произвольно.
Выбор значений диаметров окружностей вершин 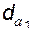 и
и 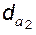 влияет на высоты зубьев
влияет на высоты зубьев 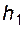 и
и 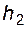 и на радиальные зазоры в зацеплении
и на радиальные зазоры в зацеплении 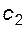 и
и 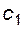 (рис. 5.12).
(рис. 5.12).
Высоту зуба каждого из колес пары можно найти по формуле
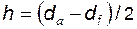 . (5.37)
. (5.37)
Радиальные зазоры у впадин первого (и соответственно второго) колеса
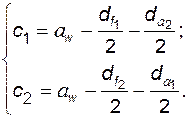 (5.38)
(5.38)
В связи с этим отметим, что существуют две наиболее распространенные системы расчета (или выбора) диаметров вершин, которые обеспечивают:
· независимую от коэффициентов смещения постоянную высоту зуба обоих колес пары, равную высоте зуба стандартного реечного контура (рис. 5.6), т.е.
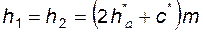 ;
;
в этом случае
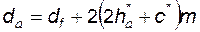 , (5.39)
, (5.39)
или, учитывая формулу (5.17),
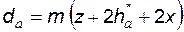 . (5.40)
. (5.40)
· независимые от коэффициентов смещения постоянные (стандартные) радиальные зазоры у впадин обоих колес пары
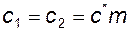 ;
;
в этом случае диаметры вершин необходимо рассчитывать по формулам
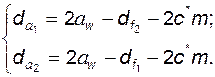 (5.41)
(5.41)
Отметим, что если нет никаких прямых указаний, следует пользоваться формулами (5.41). Также полезно знать, что при нулевом значении коэффициента суммы смещений ( 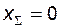 , или
, или 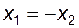 ) расчеты по формулам (5.40) и (5.41) приводят к одинаковым результатам.
) расчеты по формулам (5.40) и (5.41) приводят к одинаковым результатам.
Дата добавления: 2021-12-14; просмотров: 426;











