Эвольвента окружности, ее уравнение и свойства

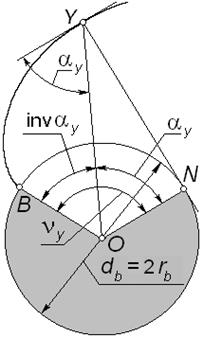
Рис. 5.2

Эвольвента окружности (в дальнейшем просто эвольвента) представляет собой траекторию любой точки прямой, перекатываемой без скольжения по окружности. Иногда эвольвенту представляют как траекторию любой точки гибкой нерастяжимой нити, сматываемой с окружности и поэтому ее часто называют разверткой окружности.

Для описания геометрии и свойств эвольвенты используют следующие термины и обозначения:

основная окружность – окружность, разверткой которой является эвольвента;

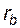(или ) – диаметр (и, соответственно, радиус) основной окружности;

B – предельная точка эвольвенты, Y– текущая точка, 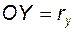– радиус-вектор текущей точки эвольвенты;

NY – производящая прямая, она же – нормаль к эвольвенте в точке Y (при этом точка N – текущий центр кривизны эвольвенты, т. е. 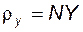– ее радиус кривизны в точке Y).

Из определения эвольвенты как развертки окружности следует, что дуга BN и длина отрезка NY одинаковы;

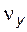– угол развернутости (центральный угол, соответствующий дуге развернутости BN);

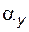– угол профиля (угол между радиус-вектором текущей точки Y эвольвенты и касательной к ней в этой точке); очевидно, что

;

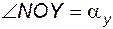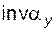– полярный угол текущей точки эвольвенты (читается – инволюта альфа игрек).

Для текущей точки Y эвольвенты, принадлежащей окружности радиуса 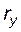, перечисленные параметры связаны соотношениями:

Угол профиля

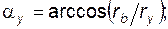(5.1)

угол развернутости (в радианах)

; (5.2)

инволюта угла профиля (полярный угол точки Y в радианах)

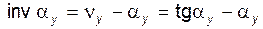; (5.3)

радиус кривизны эвольвенты в точке Y

. (5.4)

Уравнение эвольвенты в полярной параметрической форме

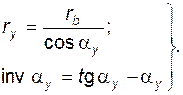(5.5)

Формулы (5.2) – (5.5) связывают между собой параметры 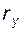, , 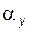, 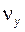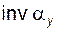и при известном диаметре основной окружности; зная любой из этих параметров, нетрудно найти остальные.