Положение нижней точки активного профиля
Сопряженные профили во время зацепления перекатываются и одновременно скользят друг по другу; при этом их контактная точка перемещается по линии зацепления – прямой 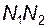 , касательной к основным окружностям зацепляющихся колес (рис. 5.13).
, касательной к основным окружностям зацепляющихся колес (рис. 5.13).
Точки контакта могут возникать и существовать только в той части 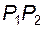 линии зацепления, которая расположена внутри окружностей вершин (эту ее часть называют активной линией зацепления - на рисунке показана двойной линией). Части сопряженных профилей зубьев, по которым происходит их взаимодействие во время зацепления, называют активными профилями(изображены также в виде двойных линий). У каждого колеса активный профиль зуба ограничен двумя точками - верхней (кромкой зуба) и нижней.
линии зацепления, которая расположена внутри окружностей вершин (эту ее часть называют активной линией зацепления - на рисунке показана двойной линией). Части сопряженных профилей зубьев, по которым происходит их взаимодействие во время зацепления, называют активными профилями(изображены также в виде двойных линий). У каждого колеса активный профиль зуба ограничен двумя точками - верхней (кромкой зуба) и нижней.
|
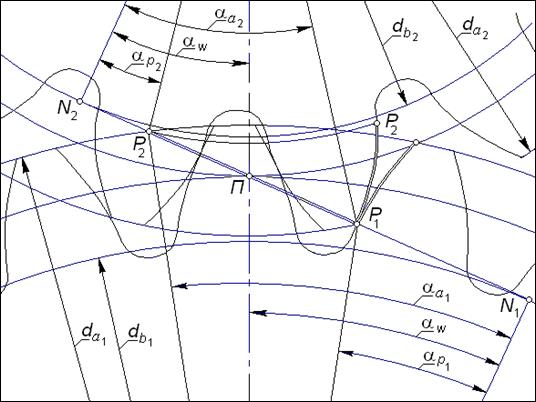
| Рис. 5.13 |
На рис. 5.13 показан момент пересопряжения зубьев – начала или окончания взаимодействия какой-либо пары профилей; в этот момент верхняя точка одного (в данном случае - второго) активного профиля контактирует с нижней точкой другого.
При проектировании передачи крайне важно уметь определять положение нижней точки активного профиля. Из того же рис. 5.13 можно найти
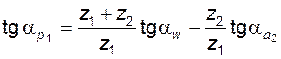 ; (5.42)
; (5.42)
тогда можно утверждать, что активный профиль зуба колеса 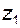 расположен между двумя концентрическими окружностями диаметров
расположен между двумя концентрическими окружностями диаметров 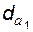 и
и
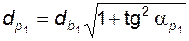 ; (5.43)
; (5.43)
из (5.42) и (5.43) нетрудно получить аналогичные формулы для парного колеса 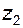 :
:
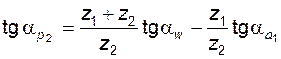 ; (5.44)
; (5.44)
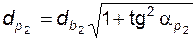 . (5.45)
. (5.45)
|
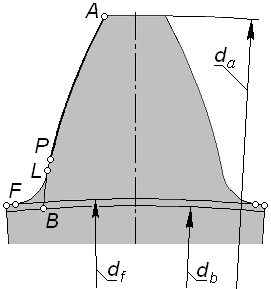
| Рис. 5.14 |
На рис. 5.14 показана структура профиля зуба эвольвентного колеса. Здесь AB – теоретическая эвольвента, а AL – фактическая; LF – переходная кривая; AP – активный профиль зуба.
Естественно, что активный профиль зуба у любого колеса, используемого в зацеплении, должен быть частью эвольвентного; это означает, что для каждого из колес, образующих пару, должно соблюдаться неравенство 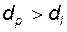 , или
, или
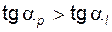 . (5.46)
. (5.46)
Нарушение неравенства (5.46) недопустимо. Опускание точки P по теоретической эвольвенте ниже точки L приведет к так называемой интерференции, при которой кромка одного зуба стремится контактировать с воображаемой (находящейся под переходной кривой) частью теоретической эвольвенты другого.
Проверка условия (5.46) имеет смысл только для колеса с неподрезанными зубьями, т.е. при 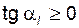 .
.
Дата добавления: 2021-12-14; просмотров: 440;











