Свойства эвольвентного зацепления
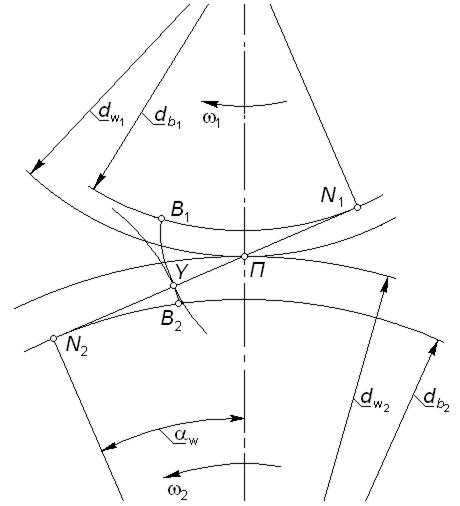
Перечислим (без доказательства) наиболее важные свойства эвольвентного внешнего зацепления (рис. 5.3):
1) две эвольвенты при межосевом расстоянии 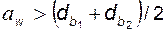 всегда взаимно сопряжены, т.е. обеспечивают передачу вращения с постоянным передаточным отношением, равным
всегда взаимно сопряжены, т.е. обеспечивают передачу вращения с постоянным передаточным отношением, равным
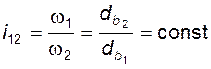 ; (5.6)
; (5.6)
2) из (5.6) следует, что кинематика эвольвентного зацепления нечувствительна к погрешности межосевого расстояния; отметим, что таким свойством обладает только эвольвентное зацепление;
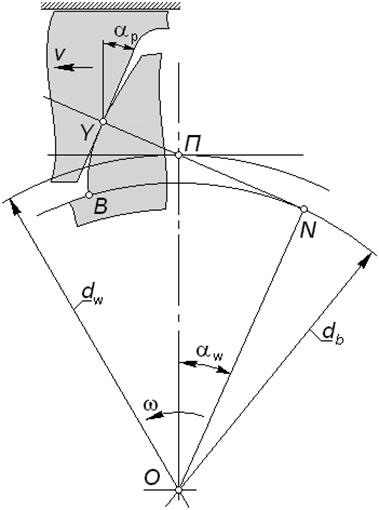
3) контактная точка Y в процессе зацепления перемещается по некоторой траектории, которую называют линией зацепления(можно также сказать, что линия зацепления является геометрическим местом контактных точек); в эвольвентном зацеплении такой линией является прямая 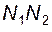 , касательная к обеим основным окружностям, она же в любой момент зацепления является и контактной нормалью;
, касательная к обеим основным окружностям, она же в любой момент зацепления является и контактной нормалью;
| 
|
| Рис. 5.3 | Рис. 5.4 |

4) угол 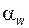 между межосевой линией и направлением касательной к профилям в контактной точке Y называют углом зацепления; в эвольвентном зацеплении угол
между межосевой линией и направлением касательной к профилям в контактной точке Y называют углом зацепления; в эвольвентном зацеплении угол 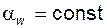 (никакое другое зацепление не обладает свойством постоянства угла
(никакое другое зацепление не обладает свойством постоянства угла 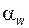 );
);
угол зацепления связан с межосевым расстоянием формулой
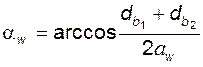 ; (5.7)
; (5.7)
5) в зубчато-реечном эвольвентном зацеплении (рис. 5.4) рейка имеет прямолинейный профиль; при этом угол профиля рейки 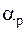 может быть любым, но каким бы он ни был, угол зацепления
может быть любым, но каким бы он ни был, угол зацепления 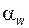 будет, очевидно, точно таким же, т.е.
будет, очевидно, точно таким же, т.е. 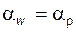 ;
;
отметим, что сопряженность такого зацепления положена в основу геометрии и кинематики процесса нарезания эвольвентных зубьев инструментом реечного типа с прямолинейным профилем зуба; если инструментальная рейка перемещается вдоль своей начальной прямой со скоростью v, а нарезаемое колесо вращается с угловой скоростью w, то в процессе такого станочного зацепления будет сформирована эвольвента окружности диаметра
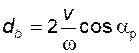 ; (5.8)
; (5.8)
|
| Рис. 5.5 |
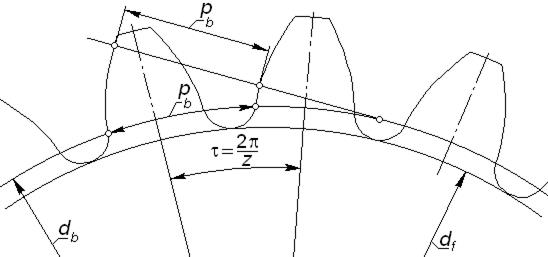
6) важным параметром эвольвентного колеса является основной шаг– расстояние 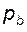 между соседними одноименными эвольвентными профилями зубьев по дуге основной окружности; величину
между соседними одноименными эвольвентными профилями зубьев по дуге основной окружности; величину 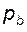 можно также измерить как расстояние между этими же эвольвентами по любой прямой, касательной к основной окружности, т.е. по нормали к обеим эвольвентам (рис. 5.5); очевидно, что два эвольвентных колеса (как и эвольвентное колесо с рейкой) могут образовать зубчатую пару только при равных основных шагах.
можно также измерить как расстояние между этими же эвольвентами по любой прямой, касательной к основной окружности, т.е. по нормали к обеим эвольвентам (рис. 5.5); очевидно, что два эвольвентных колеса (как и эвольвентное колесо с рейкой) могут образовать зубчатую пару только при равных основных шагах.
5.4. Исходный контур. Исходный
производящий контур
|
| Рис. 5.6 |
Параметры эвольвентных колес и зуборезного инструмента стандартизованы; за основу стандарта приняты параметры и очертания
зубчатой рейки с прямолинейным профилем зуба.
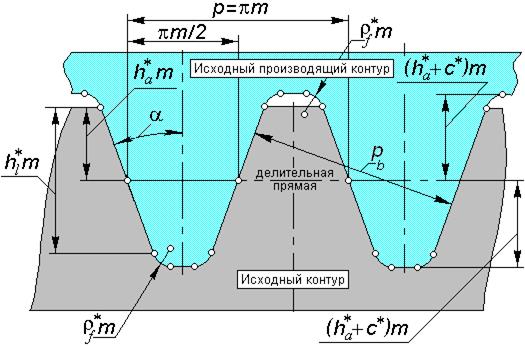
На рис. 5.6 показан так называемый исходный реечный контур (или просто исходный контур), принятый в качестве базового для определения теоретических форм и размеров стандартных зубчатых колес; он представляет собой реечный контур с равномерно чередующимися симметричными зубьями и впадинами. Для стандартных реек регламентирован угол профиля исходного контураa и его значение равно 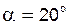 . Одну из прямых, перпендикулярных осям симметрии зубьев рейки, называют делительной прямой– на ней толщина зуба рейки равна ширине впадины.
. Одну из прямых, перпендикулярных осям симметрии зубьев рейки, называют делительной прямой– на ней толщина зуба рейки равна ширине впадины.
Профиль зуба рейки и линия ее впадин сопрягаются дугой окружности (так называемой переходной кривой).
Начальную окружность колеса в зацеплении с рейкой исходного контура называют делительной окружностью; можно показать, что если шаг рейки равен p, то диаметр d этой окружности у колеса, имеющего z зубьев, равен
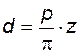 . ( 5.9)
. ( 5.9)
Отношение ( 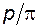 ) называют модулем и обозначают, как
) называют модулем и обозначают, как
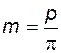 . (5.10)
. (5.10)
Модуль m измеряется в миллиметрах и его значения стандартизованы. Все линейные размеры исходных реек пропорциональны модулю:
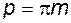 – шаг исходного контура;
– шаг исходного контура;
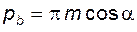 – шаг по профильной нормали (равен основному шагу сопряженного с рейкой зубчатого колеса);
– шаг по профильной нормали (равен основному шагу сопряженного с рейкой зубчатого колеса);
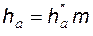 – высота делительной головки зуба;
– высота делительной головки зуба;
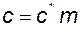 – радиальный зазор;
– радиальный зазор;
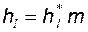 – граничная высота зуба;
– граничная высота зуба;
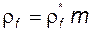 – радиус переходной кривой.
– радиус переходной кривой.
Безразмерные коэффициенты, входящие в эти формулы, имеют следующие значения: коэффициент высоты головки зуба 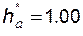 ; коэффициент радиального зазора
; коэффициент радиального зазора 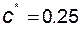 ; коэффициент граничной высоты
; коэффициент граничной высоты 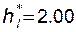 . Коэффициент радиуса переходной кривой является зависимым (рассчитываемым) параметром
. Коэффициент радиуса переходной кривой является зависимым (рассчитываемым) параметром
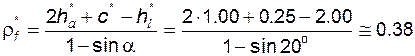 . (5.11)
. (5.11)
В тесной связи с исходным контуром находится исходный производящий контур(рис. 5.6), на основе которого строится геометрия реечного зуборезного инструмента. При нарезании зубьев таким инструментом воспроизводится зубчато-реечное станочное зацепление, в процессе которого формируются эвольвентные профили нарезаемых зубьев; геометрия этих зубьев полностью определяется взаимным расположением инструмента и заготовки, а также кинематикой станочного зацепления (или попросту – настройкой станка).
5.5. Параметры зубчатого колеса, получаемые
при нарезании зубьев
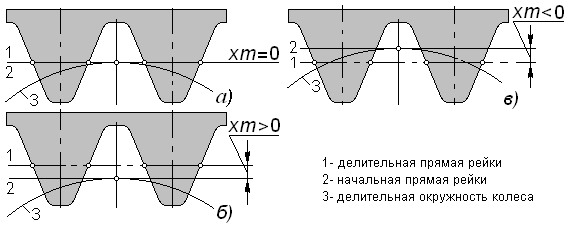
Коэффициент смещения.Взаимное положение колеса и заготовки при нарезании зубьев можно охарактеризовать положением делительной прямой инструментальной рейки относительно делительной окружности нарезаемого колеса (рис. 5.7); расстояние между ними называют смещением исходного контура, его выражают в количестве модулей, как xm.
|
| Рис. 5.7 |
Безразмерную величину x называюткоэффициентом смещения; это алгебраическая величина и здесь различают три случая, показанные рис. 5.7, а – в. Нарезая зубья при различных коэффициентах смещения, можно целенаправленно влиять на размеры и форму этих зубьев, а также на свойства колес и составленных из них передач.
Часть параметров и размеров зубчатого колеса не зависит от коэффициента смещения; к таковым относятся:
модуль m;
угол профиля эвольвенты на делительной окружности (равен углу профиля исходного контура) a;
шаг по дуге основной окружности (основной шаг)
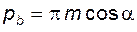 . (5.12)
. (5.12)
Значения этих трех параметров у нарезаемого колеса те же, что и у зуборезного инструмента.
Также не зависят от x:
диаметр делительной окружности (делительный диаметр)
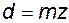 ; (5.13)
; (5.13)
диаметр основной окружности (основной диаметр)
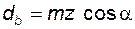 . (5.14)
. (5.14)
При нарезании зубьев поверхность их вершин не формируется, т.е. диаметр окружности вершин колеса 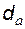 (диаметр вершин) остается равным диаметру заготовки; следовательно, нарезание зубьев – это попросту удаление материала из впадин колеса.
(диаметр вершин) остается равным диаметру заготовки; следовательно, нарезание зубьев – это попросту удаление материала из впадин колеса.
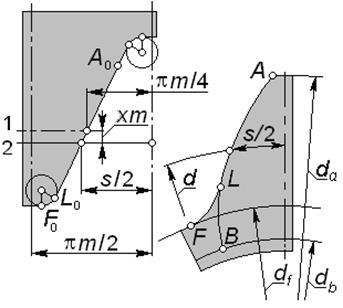
|
| а б Рис. 5.8 |
На рис. 5.8 изображены профиль зуба реечного производящего контура (а) и формируемый им при нарезании профиль зуба колеса (б). Во время нарезания начальная прямая 2 производящей рейки перекатывается без скольжения по делительной окружности колеса.
На указанных профилях отмечены соответствующие друг другу точки и участки профилей; в частности:
- эвольвентный участок AL профиля нарезаемого зуба формируется прямолинейным участком 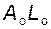 профиля зуба рейки;
профиля зуба рейки;
- переходная кривая LF на профиле зуба колеса формируется круговой кромкой 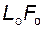 профиля зуба рейки;
профиля зуба рейки;
- вершина зуба рейки, параллельная ее делительной прямой 1, формирует окружность впадин диаметра 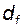 колеса.
колеса.
Очевидно, что часть профиля зуба рейки, расположенная выше точки 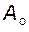 , в профилировании нарезаемого зуба не участвует.
, в профилировании нарезаемого зуба не участвует.
Найдем размеры колеса, зависящие от коэффициента смещения x:
толщина зуба по дуге делительной окружности (делительная толщина зуба) колеса
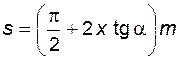 ; (5.15)
; (5.15)
диаметр окружности впадин (диаметр впадин)
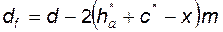 , (5.16)
, (5.16)
или
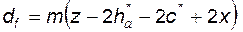 . (5.17)
. (5.17)
Важным параметром, характеризующим профиль эвольвентного зуба, является положение нижней граничной точки L эвольвенты
(рис. 5.8) – общей точки эвольвенты и переходной кривой. При нарезании зубьев указанная точка профиля формируется точкой 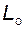 зуборезной рейки; исходя из этого для точки L наиболее просто можно найти угол профиля
зуборезной рейки; исходя из этого для точки L наиболее просто можно найти угол профиля 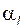 :
:
Дата добавления: 2021-12-14; просмотров: 491;











