Порядок силового анализа механизма

В данном пособии рассматриваем только такие механизмы, которые подчиняются классификации Л. В. Ассура.

До начала силового анализа необходимо выполнить структурное исследование механизма, при этом должны быть устранены местные подвижности и пассивные связи, а также произведена замена высших кинематических пар цепями с низшими парами и т.д.

Для написания формулы строения механизма должны быть выбраны начальные звенья в количестве W – это всегда те звенья, к которым приложены неизвестные внешние силы и моменты.

Формула строения полностью определяет последовательность рассмотрения частей механизма: на каждом этапе расчета может быть выполнен силовой расчет той группы или начального звена, которые являются конечными в любой ветви этой формулы. Иными словами, никакой элемент формулы строения не может быть рассчитан ранее того, который в этой формуле следует за ним.

Пусть, например, строение механизма подчиняется формуле (1.4); тогда нельзя выполнить силовой анализ группы (1 гр.) ранее (3 гр.), или группы (3 гр.) до расчета групп (4 гр.) и (6 гр.).

4.4. Методы силового анализа

Силовой расчет механизмов без учета трения в кинематических парах допускает применение как аналитических, так и графо-аналити-ческих методов.

В настоящем пособии предпочтение отдано графо-аналитическому методу планов сил.

Поскольку векторный план представляет собой графическое изображение векторного равенства, то при простой форме векторных силовых многоугольников их аналитическая обработка достаточно проста и позволяет рассчитать точные силовые соотношения для заданных положений механизмов.

4.5. Кинетостатика структурных групп II класса

Структурная группа статически определима, если для нее неизвестны только реакции во всех внешних и внутренних кинематических парах этой группы; при этом: для каждой вращательной пары неизвестны величина и направление реакции, для поступательной – величина и точка приложения.

Ниже излагается методика силового расчета групп II класса; на всех расчетных схемах звенья, составляющие группу, имеют номера
2 и 3; предполагается, что звено 2 анализируемой группы присоединяется к звену 1 механизма, а звено 3 – к звену 4.

На схемах показаны только те силы, параметры которых подлежат определению.

В символической записи уравнений планов сил будут встречаться выражения типа « 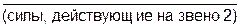». Их нужно понимать как векторную сумму всех сил, считающихся приложенными к звену 2, за вычетом реакций, определяемых при расчете этой группы (в этот перечень в общем случае входят силы веса, инерции, полезного сопротивления и реакции от звеньев ранее рассчитанных групп).

Группа 1 вида

Неизвестными являются величины и направления векторов реакций в шарнирах A, B и C.

Реакции во внешних шарнирах A и C группы раскладываем на составляющие (рис. 4.4). Реакцию в шарнире B на расчетной схеме
звена 3 направляем произвольно.

Рис. 4.4

Для определения искомых величин выполняем следующие
действия:

1) составляем уравнение моментов всех сил, действующих на звено 2, относительно оси шарнира B; в этом уравнении участвует единственная неизвестная – 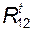, которая и определяется как алгебраическая величина;

2) для звена 3 составляем аналогичное предыдущему уравнение моментов относительно оси шарнира B; из него находим алгебраическое значение силы ;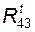

3) составляем векторное уравнение плана сил для группы:

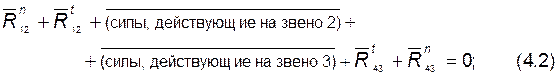
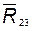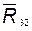в это уравнение не входит реакция (или ) в шарнире B;

в результате построения плана сил по уравнению (4.2) находим составляющие реакци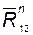й и 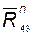, а следовательно, и полные реакци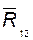и и ;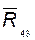

4) составляем векторное уравнение плана сил для звена 3:

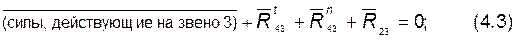
из построения плана по этому уравнению находим величину и направление реакции .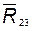

Таким образом, в результате расчета группы найдены величины и направления реакций в шарнирах A, B и C.

Группа 2 вида

Неизвестными являются: величины и направления векторов реакций в шарнирах A и B; величина и точка приложения реакции в поступательной паре.

Реакцию во внешнем шарнире A раскладываем на составляющие (рис. 4.5); реакцию в поступательной паре направляем перпендикулярно направляющей 4 и обозначаем для нее плечо относительно оси
шарнира B. Реакцию в шарнире B на расчетной схеме звена 3 направляем произвольно.

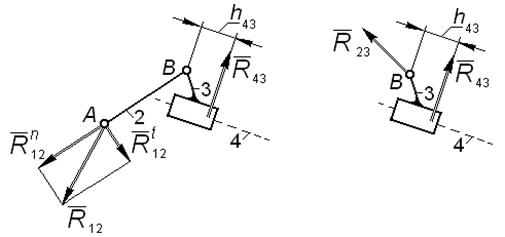
Рис. 4.5

Для определения искомых величин выполняем следующие действия:

1) составляем уравнение моментов всех сил, действующих на звено 2, относительно оси шарнира B; в этом уравнении участвует только одна неизвестная – 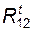, которая и определяется как алгебраическая величина;

2) составляем векторное уравнение плана сил для группы:

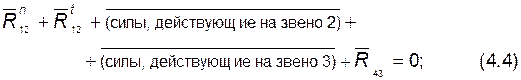
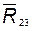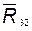в это уравнение не входит реакция (или ) в шарнире B;

из (4.4) находим составляющую реакции 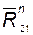(а следовательно, и полную реакцию 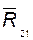) и реакцию в поступательной паре ;

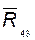3) составляем уравнение моментов сил, действующих на звено 3, относительно оси шарнира B; решая его, находим алгебраическое значение 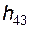– плеча реакции ;

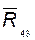4) составляем векторное уравнение плана сил для звена 3:

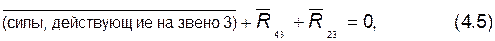
решая которое, находим величину и направление реакции .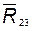

В результате расчета группы найдены все требуемые условием величины.

Группа 3 вида

Неизвестными являются величины и направления векторов реакций во внешних шарнирах A и B, а также реакция во внутренней поступательной паре и точка ее приложения.

Реакцию во внешнем шарнире A раскладываем на составляющие – вдоль линии AB и перпендикулярно ей (рис. 4.6). Реакцию в шарнире B на расчетной схеме группы направляем произвольно. Реакцию во внутренней поступательной паре направляем перпендикулярно линии относительного движения звеньев 2 и 3; на расчетной схеме звена 2 обозначаем плечо этой реакции относительно оси внешнего шарнира A.

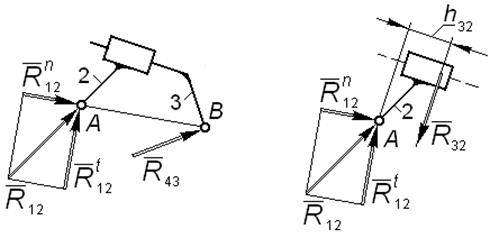
Рис. 4.6

Для нахождения неизвестных величин выполняем следующее:

1) составляем уравнение моментов относительно оси шарнира B для группы; в этом уравнении не участвует реакция во внутренней поступательной паре 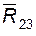(или 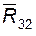); решая это уравнение, находим алгебраическую величину составляющей ;

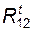2) составляем уравнение плана сил для звена 2:

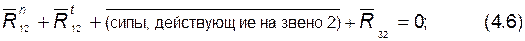
из плана сил находим составляющую 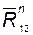(и, следовательно, полную реакцию 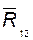) и реакцию в поступательной паре ;

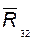3) составляем уравнение моментов относительно оси шарнира A для звена 2, решая которое, находим алгебраическую величину 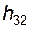– плеча реакции ;

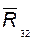4) составляем уравнение плана сил для группы:

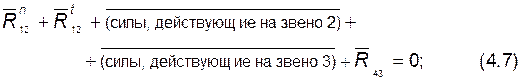
в этом уравнении не участвует реакция во внутренней поступательной паре 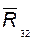(или 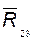); из плана сил находим величину и направление реакции .

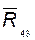Все подлежащие определению величины найдены.

Группа 4 вида

Неизвестными являются величины и точки приложения реакций во внешних поступательных парах, а также величина и направление реакции во внутренней вращательной паре A.

Реакции во внешних поступательных парах направляем перпендикулярно соответствующим направляющим и обозначаем на расчетной схеме их плечи относительно оси внутреннего шарнира A (рис. 4.7). Реакцию в шарнире A на расчетной схеме звена 3 направляем про-извольно.

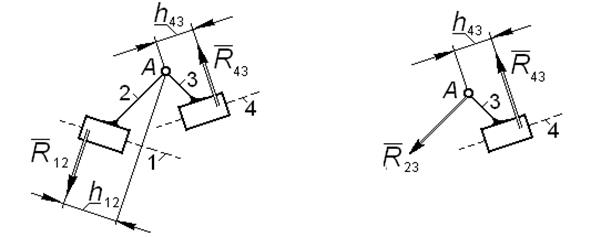
Рис. 4.7

Для нахождения неизвестных величин выполняем следующее:

1) составляем уравнение плана сил для группы:

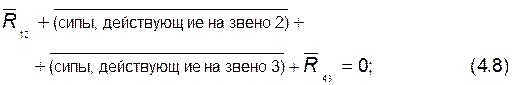
поскольку направления линий действия реакций 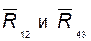известны, то из плана находим их величины;

2) составляем уравнение плана сил для звена 3:

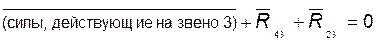; (4.9)

из плана сил по этому уравнению находим величину и направление реакции ;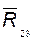

3) из уравнения моментов относительно оси шарнира A для
звена 2 найдем алгебраическое значение 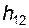– плеча реакции 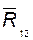относительно точки A;

4) из уравнения моментов относительно оси шарнира A для
звена 3 найдем алгебраическое значение 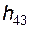– плеча реакции 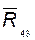относительно точки A.

Таким образом, найдены все подлежащие определению векторные и скалярные величины.

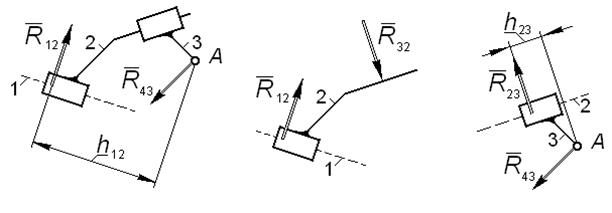
Группа 5 вида

Неизвестны величины реакций во внешней и внутренней поступательных парах, а также положение их точек приложения; неизвестны величина и направление реакции во внешней вращательной паре A
(рис. 4.8).

Рис. 4.8

Реакции в поступательных парах направляем перпендикулярно соответствующим направляющим и обозначаем их плечи относительно оси шарнира A на расчетных схемах: для реакции во внешней поступательной паре – на схеме группы, для реакции во внутренней поступательной паре – на схеме звена 3.

Реакцию в шарнире A на расчетных схемах группы и звена 3 направляем произвольно.

Для определения всех перечисленных и показанных на рис. 4.8 неизвестных выполняем следующие действия:

1) составляем уравнение плана сил для звена 2:

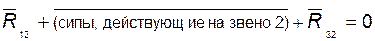; (4.10)

направления линий действия реакций в поступательных парах известны, поэтому 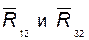находим из построения плана;

2) составляем уравнение плана сил для группы:

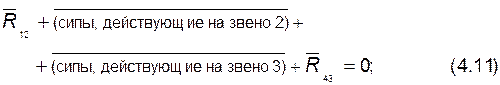
из построения плана по этому уравнению определяем величину и направление реакции 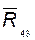во внешней вращательной паре A; в этом уравнении не участвует реакция во внутренней поступательной паре 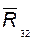(или );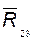

3) из уравнения моментов относительно оси шарнира A для группы определяем алгебраическую величину 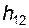– плеча реакции 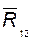относительно точки A; в этом уравнении, как и в предыдущем, не участвует реакция во внутренней поступательной паре 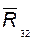(или );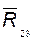

4) из уравнения моментов относительно оси шарнира A для звена 3 определяем алгебраическую величину 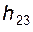– плеча реакции .

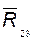Таким образом, найдены все векторные и скалярные величины, подлежащие определению.