Площадь шпангоута. Интегральные кривые Власова. Масштаб Бонжана

Формулу для определения площади погруженной части шпангоута можно получить, воспользовавшись приемом, описанным ранее при определении, например, площади ватерлинии. Выделим элемент площади шпангоута dΩ = 2ydz (рис. 1.25). Вся площадь будет равна

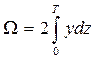. (1.79)

Если необходимо получить зависимость Ω (z), то формулу (1.79) пред-
ставляют в виде интеграла с переменным верхним пределом:

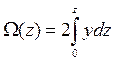. (1.80)

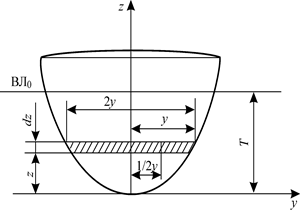
Рис. 1.25. К определению элементов площади шпангоута

Часто требуется знать не полную площадь шпангоута Ω, а половину этой площади

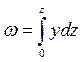, (1.81)

а также статические моменты b и с половины площади относительно
осей Oz и Оу соответственно. Согласно рис. 1.22 можно получить

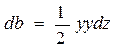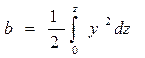; ; (1.82)

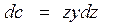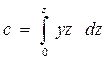; . (1.83)
Кривые ω (z), b (z) и с (z), изображенные на рис. 1.26, называются интегральными кривыми Власова. Характер этих кривых напоминает характер кривой водоизмещения. Применяют интегральные кривые в основном для нахождения водоизмещения V и координат ЦВ х_с, у_с и z_c в случае посадки судна с креном и дифферентом.

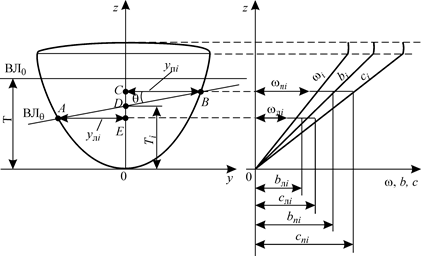
Рис. 1.26. Интегральные кривые Власова. К определению погруженной площади шпангоута для судна, сидящего с креном и дифферентом

Совокупность кривых площадей всех шпангоутов Ω называется
масштабом Бонжана. Формы масштаба Бонжана могут быть различными. Наиболее распространенная из них изображена на рис.1.27. Она получается, если на оси абсцисс отложить в каком-либо масштабе длину судна L, нанести следы шпангоутов и от них построить кривыеΩ (z).

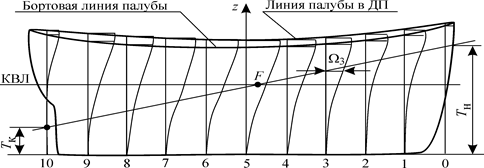
Рис. 1.27. Масштаб Бонжана

Иногда вместо кривых Ω (z) на следах шпангоутов наносят шкалы Ω(рис. 1.28). Строить такой масштаб Бонжана несколько труднее, хотя в решении практических задач пользоваться им удобнее.

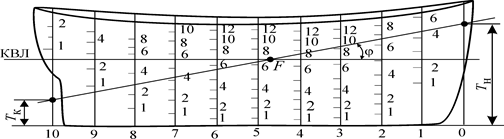
Рис. 1.28. Второй вариант масштаба Бонжана

Еще один вариант масштаба Бонжана - совмещенный - изображен на рис.1.29. Все кривые площадей шпангоутов строят при одной вертикальной оси: справа для носовых шпангоутов и мидель-шпангоута, слева для кормовых. Такой масштаб Бонжана занимает меньше места, однако пользоваться им значительно труднее, чем предыдущими.

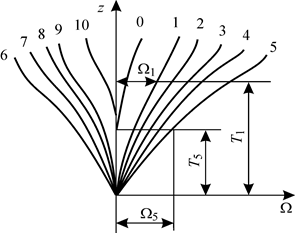
Рис. 1.29. Третий вариант масштаба Бонжана

Применяют масштаб Бонжана при определении водоизмещения V и абсциссы х_с для судна, плавающего с дифферентом.

Вычисление водоизмещения с учетом выступающих частей и соответствующей абсциссы х_с удобно производить по масштабу Бонжана, в котором к площадям шпангоутов введены поправки на выступающие части, попадающие в шпангоутное сечение. Пример учета выступающих частей приведен на рис. 1.30. На каждой ватерлинии вправо от кривой Ω (z) откладывают дополнительную площадь шпангоута ΔΩ. С учетом выступающих частей площадь шпангоута будет равна .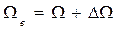

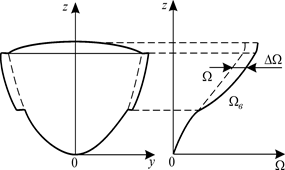
Рис. 1.30. Масштаб Бонжана с учетом выступающих частей

В последнее время в расчетах статики, входящих в САПР, исполь-
зуют видоизмененный масштаб Бонжана,на котором вместо площадей
погруженных частей шпангоутов откладывают объем заранее назначенных теоретических отсеков. Для этого выделяют двумя поперечными плоскостями, параллельными плоскости мидель - шпангоута, некоторый объем (i - ый отсек) длиной х_2i - х_1i , где х_1i и х_2i - абсциссы кормовой и носовой поперечных плоскостей сечения соответственно (рис. 1.31).Путем интегрирования по длине от кормовой оконечности (абсцисса х_к) до соответствующей абсциссы находят объемы погруженных частей корпуса

; .

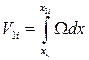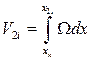Объем теоретического отсека вычисляют как разность V_2i - V_1i . Абсциссу центра тяжести объема этого отсека определяют по формуле х_i = (х_2i + х_1i)/2. На отрезке горизонтальной прямой, равной длине судна в масштабе, наносят точки, соответствующие выбранным абсциссам х_i, из которых восстанавливают перпендикуляры. Затем на каждой выбранной ватерлинии в масштабе откладывают объемы отсеков Δv_i = V_2i - V_1i . Полученное семейство кривых аналогично масштабу Бонжана. Для произвольной ватерлинии путем суммирования всех объемов отсеков легко получить объемное водоизмещение для заданных значений осадок кормой Т_к и носом Т_н. Подобные кривые могут быть построены и для статических моментов выбранных отсеков относительно координатных плоскостей, что позволяет определить координаты ЦВ.

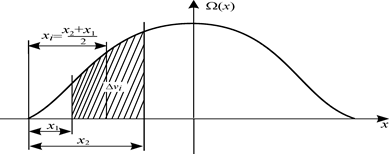
Рис. 1.31. Определение объема отсека между двумя абсциссами

1.12. Определение водоизмещения и координат ЦВдля различных случаев посадки судна. Диаграмма Фирсова

Для судна, сидящего прямо и на ровный киль, определение водо-
измещения и координат ЦВ проведено в п. 1.6. Рассмотрим, как вычисляют эти элементы для различных других случаев посадки.