Элементы площади ватерлинии
Чтобы определить V, хс , zс ,необходимо знать площади ватерлиний S и абсциссы хf центров тяжести этих площадей. Для расчета остойчивости следует вычислить моменты инерции площадей ватерлиний относительно координатных осей Ох, Оу и оси ff, проходящей через центр тяжести площади ватерлинии.
Вначале найдем элементы площади ватерлинии для судна, сидящего прямо и на ровный киль. Выделим элементарную площадь, (рис. 1.18) длиной dx и шириной 2у: dS = 2ydx, тогда
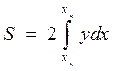 . (1.48)
. (1.48)
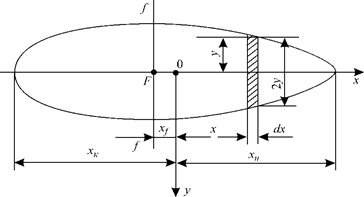
Рис. 1.18. К определению элементов площади симметричной ватерлинии
Абсцисса ЦТ площади ватерлинии равна
хf =My / S ,(1.49)
где My — статический момент площади ватерлинии относительно оси Оу. Для определения Му выпишем сначала выражение для статического момента элементарной площади dS:
dMy = xdS = x2ydx,
откуда
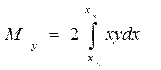 . (1.50)
. (1.50)
Получим формулы для определения осевых моментов инерции площади ватерлинии относительно главных центральных осей, одной из которых является ось Ох (в силу симметрии ватерлинии относительно Ох), другой — ось ff, параллельная оси Оу и проходящая через точку F — центр тяжести площади ватерлинии.
Найдем момент инерции dIx элементарной площади dS,для чего воспользуемся известной из теоретической механики формулой для момента инерции площади прямоугольника относительно главной центральной оси: 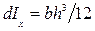 , где b = dx, h = 2y, т. e.
, где b = dx, h = 2y, т. e.
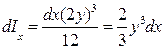 ,
,
тогда
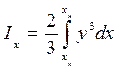 . (1.51)
. (1.51)
Момент инерции площади ватерлинии S относительно оси равен
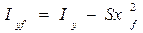 , (1.52)
, (1.52)
где Sx2f — переносный момент инерции;
1у - момент инерции площади ватерлинии относительно оси Оу, определенный по формуле
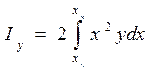 , (1.53) так как элементарный момент инерции площади dS равен
, (1.53) так как элементарный момент инерции площади dS равен 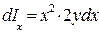 .
.
В процессе эксплуатации судно может плавать с начальным креном, когда ватерлиния несимметрична относительно ДП. Чтобы рассчитать для данного случая площадь, статические моменты, моменты инерции и другие элементы, надо несколько изменить формулы (1.36)— (1.43). С этой целью введем правые уп и левые ул ординаты (рис. 1.19).
Согласно рис. 1.19 выражение для площади элемента с учетом того, что ул отрицательна, можно записать в виде dS = yn dx— ул dx =(уп - ул) dx , а пло-щадь ватерлинии как
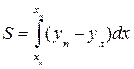 . (1.54)
. (1.54)
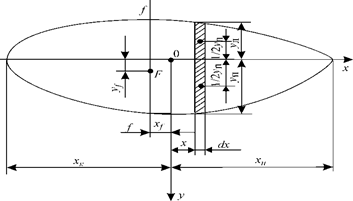
Рис. 1.19. К определению элементов площади несимметричной ватерлинии
Аналогично для статического момента площади S относительно оси Оу получим
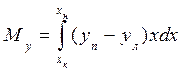 . (1.55)
. (1.55)
Тогда
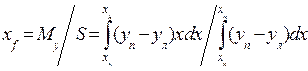 . (1.56)
. (1.56)
Для несимметричной ватерлинии статический момент площади относительно оси Ох не равен нулю. Статический момент для правой элементарной площадки равен
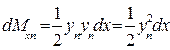 ,
,
для левой –
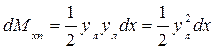 ,
,
суммарный -
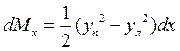 .
.
Тогда формула для полного статического момента запишется в виде
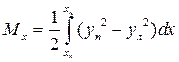 . (1.57)
. (1.57)
Центр тяжести F площади ватерлинии будет находиться от ДП на расстоянии
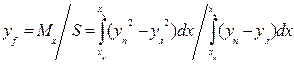 . (1.58)
. (1.58)
Для моментов инерции элементарной площадки можно записать следующие выражения:
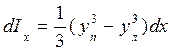 ;
; 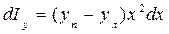 .
.
Следовательно, моменты инерции относительно осей координат будут равны
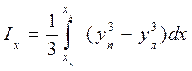 ; (1.59)
; (1.59)
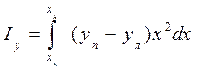 . (1.60)
. (1.60)
Но в дальнейших расчетах нам потребуются моменты инерции относительно осей, проходящих через ЦТ F площади ватерлинии. Они определяются с учетом соответствующих переносных моментов инерции по формулам
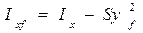 ;
;
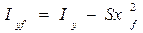 . (1.61)
. (1.61)
Формулы (1.54) - (1.61) имеют более общий характер, чем соответствующие формулы, полученные для симметричного судна. Для него уп = - ул ивыражения (1.54) - (1.61) переходят в (1.46) - (1.53).
Формула (1.57) позволяет вычислить также статический момент погруженного объема Мxz несимметричного судна относительно ДП, а затем и ординату ЦВ ус. Статический момент может быть представлен как интегральная сумма статических моментов элементарных объемов
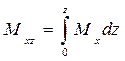 ,
,
или с учетом (1.57)
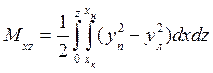 .
.
Ордината ЦВ
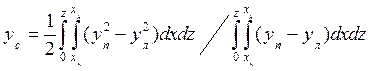 . (1.62)
. (1.62)
Необходимо отметить, что использование формул (1.54) - (1.62) предполагает незначительную несимметрию относительно ДП, поэтому можно пре-небречь центробежным моментом инерции, т.е. Ixy 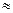 0 .
0 .
При вычислениях элементов площади ватерлиний многокорпусных плавучих объектов (плавучие буровые установки, трисеки и т.д.) используются два основных метода, применение каждого из которых зависит от особенностей формы площадок, составляющих ватерлинию.
Если ватерлиния состоит из площадок сложной формы, в том числе и характерной для ватерлиний обычных судов (например, рис. 1.20), можно использовать подход, продемонстрированный при выводе формул (1.54) - (1.62). Тогда получим:
S= 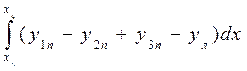 ; (1.63)
; (1.63)
Mx= 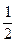
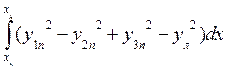 ; (1.64)
; (1.64)
My= 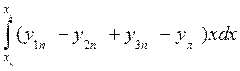 (1.65)
(1.65)
I x = 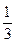
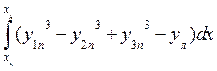 ; (1.66)
; (1.66)
Iy = 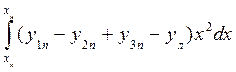 . (1.67)
. (1.67)
Величины xf , yf , Ixf и Iyf определяются по формулам (1.56), (1.58) и (1.61).
При большом числе корпусов формулы (1.63) - (1.67) можно обобщить.
Тогда получим:
S = 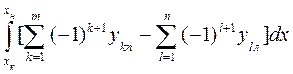 ; (1.68)
; (1.68)
Mx = 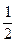
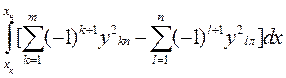 ; (1.69)
; (1.69)
My = 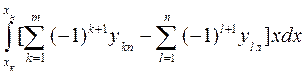 ; (1.70)
; (1.70)
Ix= 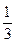
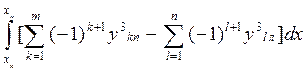 ; (1.71)
; (1.71)
Iy = 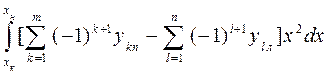 . (1.72)
. (1.72)
Здесь m - число правых ординат, k – текущий номер правой ординаты, n - число левых ординат, l – текущий номер левой ординаты. Величины xf , yf , Ixf и Iyf определяются по формулам (1.56), (1.58) и (1.61).
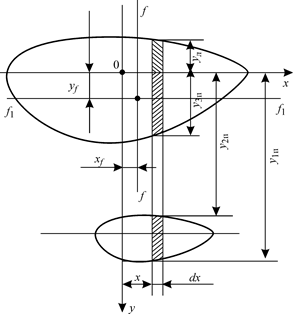
Рис. 1.20. К определению элементов площади ватерлинии, состоящей из
площадок сложной формы
Если же ватерлиния состоит из площадок простой формы (круг, эллипс, прямоугольник и т.д.), для которых можно заранее рассчитать характеристики площади относительно собственных центральных осей (sk - площадь, ixk - момент инерции площади относительно собственной центральной оси Ok¢хk¢, параллельной главной оси Ox; iyk - момент инерции площади относительно собственной центральной оси Ok¢уk¢, параллельной главной центральной оси Oy (см. рис. 1.21), то получатся следующие формулы :
S = 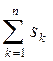 ; Ix =
; Ix = 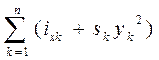 ; Iy=
; Iy= 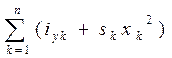 ;
;
My = 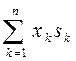 ; Mx=
; Mx= 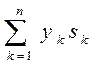 , (1.73)
, (1.73)
где n - число площадок, составляющих площадь ватерлинии.
Здесь также предполагается, что центробежный момент инерции Ixy = 0.
Величины xf , yf , Ixf , Iyf определяются по формулам (1.56), (1.58) и (1.61).
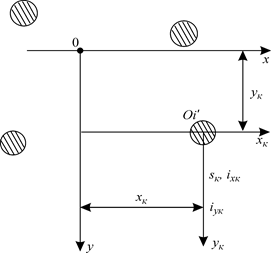
Рис. 1.21. К определению элементов площади ватерлинии, состоящей из
площадок простой формы
Дата добавления: 2021-12-14; просмотров: 647;











