Посадка судна с креном и дифферентом

В этом случае удобно пользоваться интегральными кривыми Власова. С их помощью определяют полную площадь погруженной части шпангоута Ω, ее статический момент В относительно оси Oz и статический момент С относи-тельно оси Оу с учетом крена и дифферента.

Осадку каждого i-го шпангоута вычисляют по третьей формуле (1.16):

Т_i = T_м + 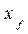tgψ .

Вывод формулы для определенияΩ рассмотрим более подробно. На оси Oz (см. рис. 1.26) откладывают Т_i и через точку D проводят наклонную ватерлинию В_θЛ_θ под углом крена θ. Площадь шпангоута 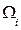можно представить в виде суммы площадей:

.

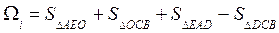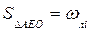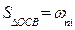Обозначая и , определяют их значения по кривой 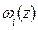,как это показано на рис. 1.23. В ΔDCB СВ = y_пi , CD = y_ni tg θ ; в ΔАED AE = у_лi , DE = у_лt tg θ , где y_ni и у_лi - ординаты шпангоута. Тогд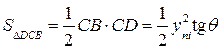а , а .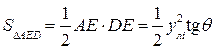

Окончательно

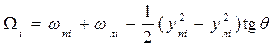. (1.84)

Статические моменты относительно оси Oz для указанных площадей
определяют аналогичным образом. Суммарный статический момент площади погруженной части шпангоута сучетом знака у_лi и того, что статические моменты площадей слева от оси Oz отрицательны, равен

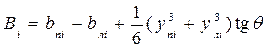. (1.85)

Суммарный статический момент относительно оси Оу с учетом(1.16) будет равен

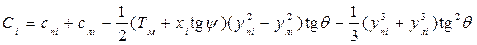. (1.86)

Формулы (1.84) - (1.86) верны и для случая посадки на ровный киль с креном, только в этом случае ψ = 0 и T_i = Т_м для всех шпангоутов.

Если известны Ω, В и С, можно определить водоизмещение и ста-
тические моменты:

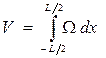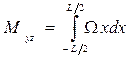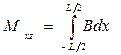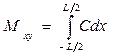; ; ; ,(1.87)

а затем координаты ЦВ по формулам (1.34):

; ; .

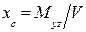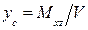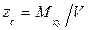Диаграмму Фирсова можно строить и с использованием интегральных кри-вых Власова при θ = 0. Но наиболее удобно рассчитывать с их помощью кривые аппликат ЦВв зависимости от осадок носом и кормой: z_c = f (T_н , Т_к). Семейство этих кривых образует диаграмму, аналогичную диаграмме Фирсова (рис. 1.33). Построение этой диаграммы проводят так же, как и диаграммы Фирсова.

Влияние угла крена на V, х_с , z_с мало (особенно при малых углах),
поэтому можно пользоваться диаграммой Фирсова и диаграммой аппликат ЦВ, рассчитанными при θ = 0, и для накрененного судна.

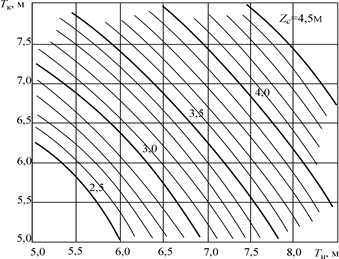
Рис. 1.33. Диаграмма аппликат ЦВ