Кривые абсцисс ЦВ и ЦТ площадей ватерлиний. Кривая аппликат ЦВ

С изменением осадки судна изменяются форма и объем подводной
части корпуса, вследствие чего меняются значения абсцисс ЦВ х_с и центров тяжести площади ватерлинии x_f.. Для определения функции х_с (z) применяют видоизмененную формулу (1.30), подставив в нее вместо Т в качестве верхнего предела z :

.

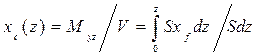Зависимость x_f (z) находят по формуле (1.49), проводя расчеты последова-тельно для всех ватерлиний.

Для построения кривых х_с (z) и x_f (z) на соответствующих ватерлиниях откладывают в одинаковом масштабе значения х_с и x_f (положительные вправо от вертикальной оси Oz, отрицательные - влево) и полученные точки соединяют плавными кривыми. Кривая x_f (z) следует за обводами корпуса и при резком их изменении получает излом. Кривая х_с (z) имеет более плавный характер. В точке пересечения х_с (z) и x_f (z) должен быть экстремум функции х_с (z) (см. рис. 1.22)

Рассмотрим этот вопрос подробнее. Составим выражения для производной от х_с (z) по z:

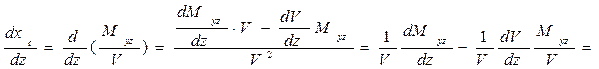
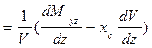. (1.74)

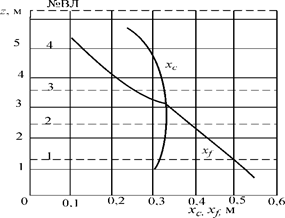
Рис. 1.22. Кривые х_с (z) и x_f (z)

Так как статический момент равен 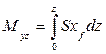, его производная по z имеет вид 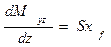. К тому же .

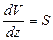Следовательно,

.

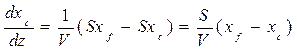Условие для определения экстремума 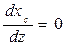выполняется только в том случае, если х_f = х_с , т. е. в точке пересечения кривых будет максимум или минимум х_с (z) .

Из формулы (1.74) с учетом (1.32) можно также получить

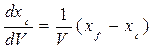. (1.75)

Эта формула используется в дальнейшем.

Зависимость аппликаты ЦВ от осадки можно определить по видоизме-ненной формуле (1.37)

.

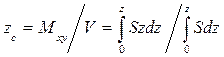Кривая z_c (z) no форме напоминает грузовой размер. Производная аппликаты ЦВ по осадке равна

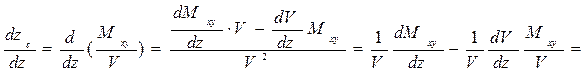
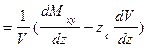. (1.76)

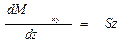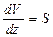С учетом того, что и , выражение (1.76) можно переписать в виде

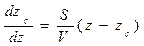. (1.77)

Так как всегда z_c < z , не может быть получено условие 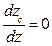, т.е. кривая 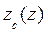не имеет экстремумов (рис.1.23).

Из формулы (1.77) можно получить зависимость

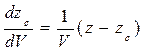, (1.78)

применяющуюся в дальнейшем.

Если все шпангоуты судна имеют форму прямоугольников, то z_c = z/2. Если же все шпангоуты имеют форму треугольников, то z_c = 2z/3. У обычных судов обводы имеют форму, промежуточную между прямоугольной и треугольной, поэтому практически z/2 ≤ z_c ≤ 2z/3.

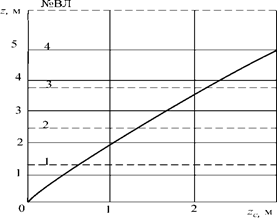
Рис. 1.23. Кривая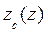

В последние годы появились суда с подповерхностными корпусами (трисеки, плавучие буровые установки и т. д.). Для таких судов значение z_c может быть гораздо меньше половины осадки (рис. 1.24).

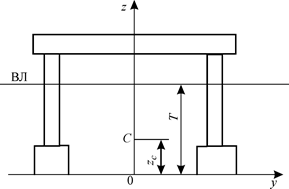
Рис. 1.24. Положение ЦВ по высоте для судна с подповерхностными

корпусами.