Вычисление площадей плоских фигур

Как с помощью определенного интеграла вычислить площадь плоской фигуры.

Для этого надо:

1) Разбираться в неопределенном интеграле хотя бы на среднем уровне.

2) Уметь применять формулу Ньютона-Лейбница и вычислять определенный интеграл.

3) Знать два правила:

-Определенный интеграл численно равен площади соответствующей криволинейной трапеции.

-Если на отрезке 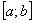некоторая непрерывная функция 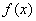больше либо равна некоторой непрерывной функции 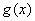, то площадь фигуры, ограниченной графиками данных

функций и прямыми 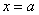, , 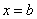можно найти по формуле: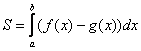

Вспомним, что криволинейной трапецией называется плоская фигура, ограниченная осью 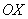, прямыми 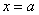, 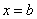и графиком непрерывной на отрезке 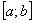функции 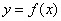, которая не меняет знак на этом промежутке. Пусть данная фигура расположена не ниже оси абсцисс:

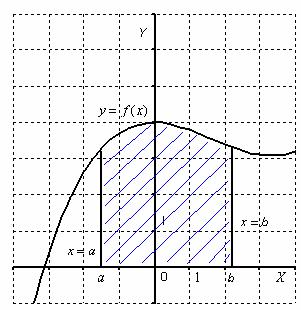
Тогда площадь криволинейной трапеции численно равна определенному интегралу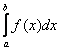. С точки зрения геометрии определенный интеграл – это ПЛОЩАДЬ.

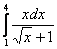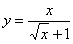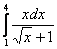То есть, определенному интегралу (если он существует) геометрически соответствует площадь некоторой фигуры. Например, рассмотрим определенный интеграл . Подынтегральная функция задает на плоскости кривую, располагающуюся выше оси (желающие могут выполнить чертёж), а сам определенный интеграл численно равен площади соответствующей криволинейной трапеции.

Пример 1

Вычислить площадь фигуры, ограниченной линиями , , , .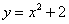

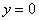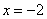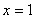Выполним чертеж (обратите внимание, что уравнение 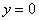задает ось ):

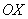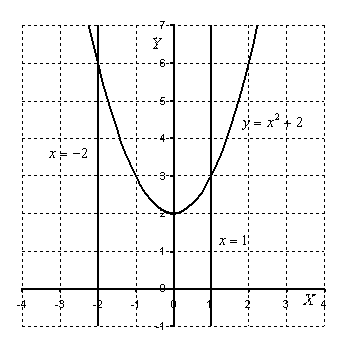
На отрезке 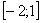график функции 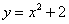расположен над осью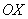, поэтому:

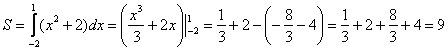
Ответ: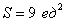

Пример 2

Вычислить площадь фигуры, ограниченной линиями 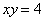, , 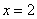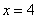и осью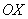

Это пример для самостоятельного решения.

Что делать, если криволинейная трапеция расположена под осью ?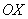

Пример 3

Вычислить площадь фигуры, ограниченной линиями 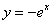, 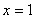и координатными осями.

Решение: Выполним чертеж:

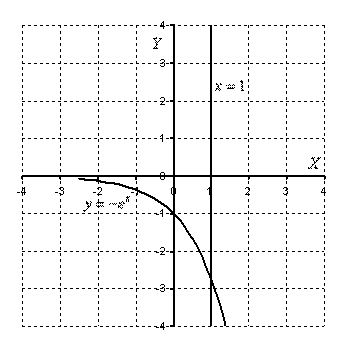
Если криволинейная трапеция расположенапод осью (или, по крайней мере, не выше данной оси), то её площадь можно найти по формуле: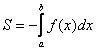
В данном случае:

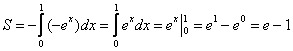
Ответ: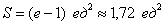

На практике чаще всего фигура расположена и в верхней и в нижней полуплоскости.

Пример 4

Найти площадь плоской фигуры, ограниченной линиями , .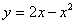

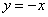Решение: Сначала нужно выполнить чертеж.

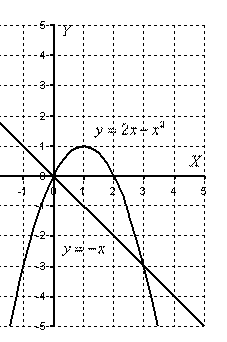
А теперь формула: Если на отрезке 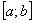некоторая непрерывная функция 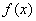больше либо равна некоторой непрерывной функции 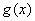, то площадь фигуры, ограниченной графиками данных функций и прямыми 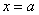, , 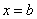можно найти по формуле: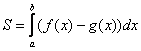

В рассматриваемом примере очевидно, что на отрезке 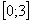парабола располагается выше прямой, а поэтому из 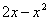необходимо вычесть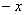

Искомая фигура ограничена параболой 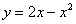сверху и прямой 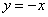снизу.
На отрезке 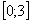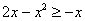, по соответствующей формуле:

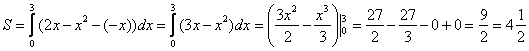
Ответ: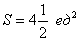

Примеры для самостоятельного решения

Пример 5

Найти площадь фигуры, ограниченной линиями , .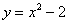

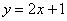Пример 6

Найти площадь фигуры, ограниченной линиями , .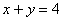

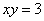Дата добавления: 2020-06-09; просмотров: 432;